TL;DR
See title.
Motivation
I am hoping for a canonical answer along the lines of "(1) No, (2) Not applicable, because (1)", which we can use to close many wrong questions about unbalanced datasets and oversampling. I would be quite as happy to be proven wrong in my preconceptions. Fabulous Bounties await the intrepid answerer.
My argument
I am baffled by the many questions we get in the unbalanced-classes tag. Unbalanced classes seem to be self-evidently bad. And oversampling the minority class(es) is quite as self-evidently seen as helping to address the self-evident problems. Many questions that carry both tags proceed to ask how to perform oversampling in some specific situation.
I understand neither what problem unbalanced classes pose, nor how oversampling is supposed to address these problems.
In my opinion, unbalanced data do not pose a problem at all. One should model class membership probabilities, and these may be small. As long as they are correct, there is no problem. One should, of course, not use accuracy as a KPI to be maximized in a classification problem. Or calculate classification thresholds. Instead, one should assess the quality of the entire predictive distribution using proper scoring-rules. Tetlock's Superforecasting serves as a wonderful and very readable introduction to predicting unbalanced classes, even if this is nowhere explicitly mentioned in the book.
Related
The discussion in the comments has brought up a number of related threads.
- What problem does oversampling, undersampling, and SMOTE solve? IMO, this question does not have a satisfactory answer. (Per my suspicion, this may be because there is no problem.)
- When is unbalanced data really a problem in Machine Learning? The consensus appears to be "it isn't". I'll probably vote to close this question as a duplicate of that one.
IcannotFixThis' answer, seems to presume (1) that the KPI we attempt to maximize is accuracy, and (2) that accuracy is an appropriate KPI for classification model evaluation. It isn't. This may be one key to the entire discussion.
AdamO's answer focuses on the low precision of estimates from unbalanced factors. This is of course a valid concern and probably the answer to my titular question. But oversampling does not help here, any more than we can get more precise estimates in any run-of-the-mill regression by simply duplicating each observation ten times.
What is the root cause of the class imbalance problem? Some of the comments here echo my suspicion that there is no problem. The single answer again implicitly presumes that we use accuracy as a KPI, which I find unsatisfactory.
Are there Imbalanced learning problems where re-balancing/re-weighting demonstrably improves accuracy? is related, but presupposes accuracy as an evaluation measure. (Which I argue is not a good choice.)
Summary
The threads above can apparently be summarized as follows.
- Rare classes (both in the outcome and in predictors) are a problem, because parameter estimates and predictions have high variance/low precision. This cannot be addressed through oversampling. (In the sense that it is always better to get more data that is representative of the population, and selective sampling will induce bias per my and others' simulations.)
- Rare classes are a "problem" if we assess our model by accuracy. But accuracy is not a good measure for assessing classification models. (I did think about including accuracy in my simulations, but then I would have needed to set a classification threshold, which is a closely related wrong question, and the question is long enough as it is.)
An example
Let's simulate for an illustration. Specifically, we will simulate ten predictors, only a single one of which actually has an impact on a rare outcome. We will look at two algorithms that can be used for probabilistic classification: logistic-regression and random-forests.
In each case, we will apply the model either to the full dataset, or to an oversampled balanced one, which contains all the instances of the rare class and the same number of samples from the majority class (so the oversampled dataset is smaller than the full dataset).
For the logistic regression, we will assess whether each model actually recovers the original coefficients used to generate the data. In addition, for both methods, we will calculate probabilistic class membership predictions and assess these on holdout data generated using the same data generating process as the original training data. Whether the predictions actually match the outcomes will be assessed using the Brier score, one of the most common proper scoring rules.
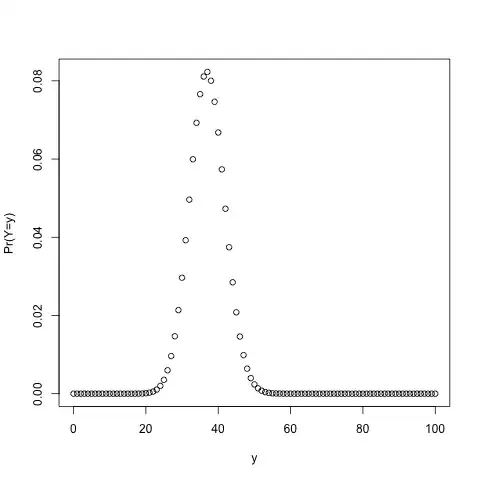
We will run 100 simulations. (Cranking this up only makes the beanplots more cramped and makes the simulation run longer than one cup of coffee.) Each simulation contains $n=10,000$ samples. The predictors form a $10,000\times 10$ matrix with entries uniformly distributed in $[0,1]$. Only the first predictor actually has an impact; the true DGP is
$$ \text{logit}(p_i) = -7+5x_{i1}. $$
This makes for simulated incidences for the minority TRUE class between 2 and 3%:
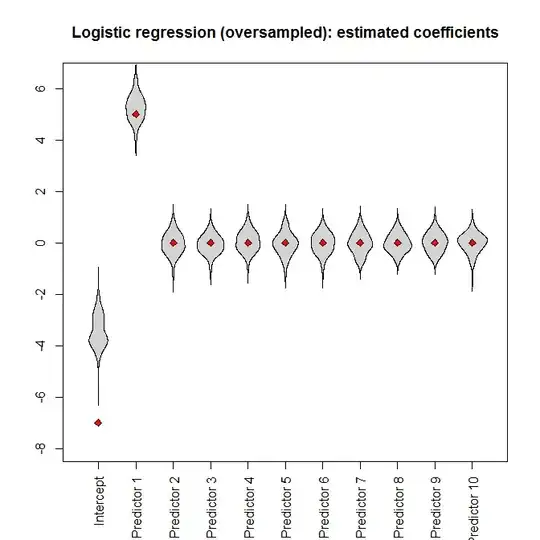
Let's run the simulations. Feeding the full dataset into a logistic regression, we (unsurprisingly) get unbiased parameter estimates (the true parameter values are indicated by the red diamonds):
However, if we feed the oversampled dataset to the logistic regression, the intercept parameter is heavily biased:
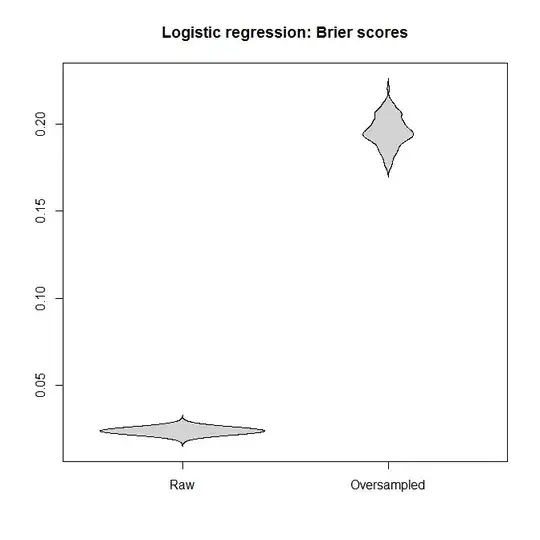
Let's compare the Brier scores between models fitted to the "raw" and the oversampled datasets, for both the logistic regression and the Random Forest. Remember that smaller is better:
In each case, the predictive distributions derived from the full dataset are much better than those derived from an oversampled one.
I conclude that unbalanced classes are not a problem, and that oversampling does not alleviate this non-problem, but gratuitously introduces bias and worse predictions.
Where is my error?
A caveat
I'll happily concede that oversampling has one application: if
- we are dealing with a rare outcome, and
- assessing the outcome is easy or cheap, but
- assessing the predictors is hard or expensive
A prime example would be genome-wide association studies (GWAS) of rare diseases. Testing whether one suffers from a particular disease can be far easier than genotyping their blood. (I have been involved with a few GWAS of PTSD.) If budgets are limited, it may make sense to screen based on the outcome and ensure that there are "enough" of the rarer cases in the sample.
However, then one needs to balance the monetary savings against the losses illustrated above - and my point is that the questions on unbalanced datasets at CV do not mention such a tradeoff, but treat unbalanced classes as a self-evident evil, completely apart from any costs of sample collection.
R code
library(randomForest)
library(beanplot)
nn_train <- nn_test <- 1e4
n_sims <- 1e2
true_coefficients <- c(-7, 5, rep(0, 9))
incidence_train <- rep(NA, n_sims)
model_logistic_coefficients <-
model_logistic_oversampled_coefficients <-
matrix(NA, nrow=n_sims, ncol=length(true_coefficients))
brier_score_logistic <- brier_score_logistic_oversampled <-
brier_score_randomForest <-
brier_score_randomForest_oversampled <-
rep(NA, n_sims)
pb <- winProgressBar(max=n_sims)
for ( ii in 1:n_sims ) {
setWinProgressBar(pb,ii,paste(ii,"of",n_sims))
set.seed(ii)
while ( TRUE ) { # make sure we even have the minority
# class
predictors_train <- matrix(
runif(nn_train*(length(true_coefficients) - 1)),
nrow=nn_train)
logit_train <-
cbind(1, predictors_train)%*%true_coefficients
probability_train <- 1/(1+exp(-logit_train))
outcome_train <- factor(runif(nn_train) <=
probability_train)
if ( sum(incidence_train[ii] <-
sum(outcome_train==TRUE))>0 ) break
}
dataset_train <- data.frame(outcome=outcome_train,
predictors_train)
index <- c(which(outcome_train==TRUE),
sample(which(outcome_train==FALSE),
sum(outcome_train==TRUE)))
model_logistic <- glm(outcome~., dataset_train,
family="binomial")
model_logistic_oversampled <- glm(outcome~.,
dataset_train[index, ], family="binomial")
model_logistic_coefficients[ii, ] <-
coefficients(model_logistic)
model_logistic_oversampled_coefficients[ii, ] <-
coefficients(model_logistic_oversampled)
model_randomForest <- randomForest(outcome~., dataset_train)
model_randomForest_oversampled <-
randomForest(outcome~., dataset_train, subset=index)
predictors_test <- matrix(runif(nn_test *
(length(true_coefficients) - 1)), nrow=nn_test)
logit_test <- cbind(1, predictors_test)%*%true_coefficients
probability_test <- 1/(1+exp(-logit_test))
outcome_test <- factor(runif(nn_test)<=probability_test)
dataset_test <- data.frame(outcome=outcome_test,
predictors_test)
prediction_logistic <- predict(model_logistic, dataset_test,
type="response")
brier_score_logistic[ii] <- mean((prediction_logistic -
(outcome_test==TRUE))^2)
prediction_logistic_oversampled <-
predict(model_logistic_oversampled, dataset_test,
type="response")
brier_score_logistic_oversampled[ii] <-
mean((prediction_logistic_oversampled -
(outcome_test==TRUE))^2)
prediction_randomForest <- predict(model_randomForest,
dataset_test, type="prob")
brier_score_randomForest[ii] <-
mean((prediction_randomForest[,2]-(outcome_test==TRUE))^2)
prediction_randomForest_oversampled <-
predict(model_randomForest_oversampled,
dataset_test, type="prob")
brier_score_randomForest_oversampled[ii] <-
mean((prediction_randomForest_oversampled[, 2] -
(outcome_test==TRUE))^2)
}
close(pb)
hist(incidence_train, breaks=seq(min(incidence_train)-.5,
max(incidence_train) + .5),
col="lightgray",
main=paste("Minority class incidence out of",
nn_train,"training samples"), xlab="")
ylim <- range(c(model_logistic_coefficients,
model_logistic_oversampled_coefficients))
beanplot(data.frame(model_logistic_coefficients),
what=c(0,1,0,0), col="lightgray", xaxt="n", ylim=ylim,
main="Logistic regression: estimated coefficients")
axis(1, at=seq_along(true_coefficients),
c("Intercept", paste("Predictor", 1:(length(true_coefficients)
- 1))), las=3)
points(true_coefficients, pch=23, bg="red")
beanplot(data.frame(model_logistic_oversampled_coefficients),
what=c(0, 1, 0, 0), col="lightgray", xaxt="n", ylim=ylim,
main="Logistic regression (oversampled): estimated
coefficients")
axis(1, at=seq_along(true_coefficients),
c("Intercept", paste("Predictor", 1:(length(true_coefficients)
- 1))), las=3)
points(true_coefficients, pch=23, bg="red")
beanplot(data.frame(Raw=brier_score_logistic,
Oversampled=brier_score_logistic_oversampled),
what=c(0,1,0,0), col="lightgray", main="Logistic regression:
Brier scores")
beanplot(data.frame(Raw=brier_score_randomForest,
Oversampled=brier_score_randomForest_oversampled),
what=c(0,1,0,0), col="lightgray",
main="Random Forest: Brier scores")