I have an unbalanced dataset with 3969 rows of customer data. The labels are whether or not they subscribed for a loan (yes or no). There are 3618 no cases (91.2%) and 351 yes cases (8.8%). I am more interested in predicting yes than no.
My question concerns finding an appropriate benchmark or naive prediction against which to compare my models. (I am mainly working with decision trees, but I don't think that is relevant to my question.) I understand that because the data is heavily unbalanced, the naive prediction would be to assign all cases as no, which would give a prediction accuracy of 91.2%; thus, any model I develop must have greater than 91.2% accuracy. Here are the results of my initial analysis (of a 30% validation set after model development on a 70% training set of the data):
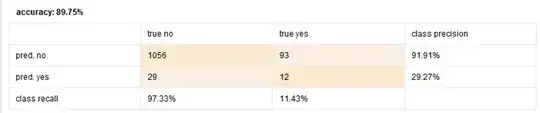
Here, the overall accuracy of 89.75% is less than 91.2%, so I consider this a bad model overall. However, I am primarily interested in the predictions of the yes cases. For this initial model, the class recall for yes is 11.43%. That is, the original dataset had 8.8% yes data, and this model can predict yes 11.43% of the time. Is this good or bad? Is it even relevant to my intention of identifying yes cases? Or does "good or bad" depend entirely on how much weight or cost I assign to finding yes versus missing no?
As a second step, I know that my poor accuracy results are because many algorithms struggle with unbalanced data. So, I undersampled the training set (not the entire dataset) to obtain a 50-50 proportion across yes and no cases and then built a new model on that undersampled data. Here are the results of my analysis of this balanced dataset (the 30% validation set after model development on the undersampled training set:
Since this data is balanced, I understand that the naive benchmark for accuracy is 50%. So, the accuracy of 70.5% is a good overall result. The class recall for yes of 54.29% is also a good result, and so this second model is undoubtedly superior to the first. However, my second question again concerns the benchmark for comparison of the class recall for yes. Am I supposed to compare that against the initial dataset distribution of 8.8% yes, or is there some other naive benchmark for this value? I am fairly certain that I should not be comparing the class recall with 50% because the validation dataset was not balanced; only the training dataset was.
So, in summary, what is the appropriate naive benchmark against which to compare class recall results in binary classification for an unbalanced dataset?