I have been struggling with this topic for a while, and on this site are multiple answers but none of them answers completely my question. For example in Which class to define as positive in unbalanced classification states that all classification algorithms are symmetrical in regard to which class is called positive and which is called negative, or which is assigned to 0 and which to 1. My question goes a little further:
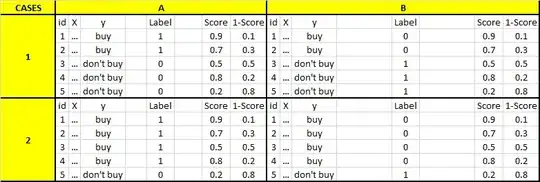
Does the probability change when you define the label? I understand that algorithms are symmetrical in regard to which class is called positive/negative, but that doesn't mean that the probability is the same if you change the label (or it does?, I have always labeled as 1 the class I'm focused to predict, so I assumed that 0.9 probability meant that it's likely to be 1, and if I labeled as 0 the probability would be 0.1). To be more specific, we have these four Cases: 1A, 1B, 2A, 2B and to avoid misunderstandings we will define them as positive class = buy and negative class= don't buy.
In the table above we have for each case an id, multiple variables in X and an independent variable y. The difference between cases A and B is how the label is defined: for A, buy=1 and don't buy=0 and vice versa for B, for 1 are balanced datasets and 2 unbalanced datasets. Once the label is defined, we run a classification algorithm that gives the Score or 1-Score column.
So, my questions:
Q1: I define the positive class as 1 (like in Case 1A), we run some classification algorithm, and we get the
Scorecolumn. Then, if I define the positive class as 0 (like in Case 1B), we run some classification algorithm, do I get theScorecolumn or the1-Scorecolumn? I always thought that the algorithm gives youScoreorScore-1depending on how you classify (as 0 or 1) the positive/negative class. In other words, I thought the algorithm will always give you the highest probabilities of the class (positive or negative) that you defined as 1. Is this right or the classification algorithm will always give you the same probability independently of how you classify (as 0 or 1) the positive/negative class? (for this question you could use the observations from the table above withid=1andid=4, as bothScorehave high probability but they are different classes and for cases A and B they are labeled differently)Q2: ¿Every? algorithm has a loss function to minimize, once the algorithm finishes minimizing we measure the model performance with an evaluation metric. The scores are computed by the loss function, so the probabilities (or the scores columns in the table above) are dependent on the loss function and independent from the evaluation metric. If I'm right with this statement, my question is: If I have unbalanced data, does any loss function consider unbalanced data or the loss function minimize the same way no matter how unbalanced is the data? and going further, does the loss function changes its minimization if we change how we classify the label (as 0 or 1, like case 2A vs 2B) and the data is unbalanced? (I understand we shouldn't use SMOTE to balance the data but rather to use the appropriate statistical tool for unbalanced data as you can see here, here, here or here)