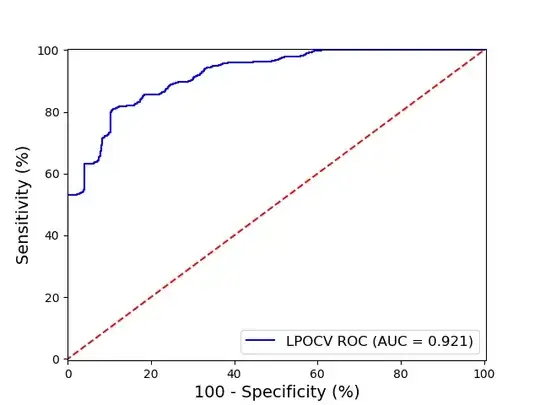
My dataset consists of 150 patients where 50 are controls/healthy (negative) and 100 are sick (positive).
If I want my model to have high sensitivity at high specificity (left side of the ROC), in other words to have low false positive rates, should I correct my model by applying weights to it? Because usually the positive class is the minority class and I see why you need to correct for it but should I in my case?