How do you know that your classifier is suffering from class imbalance?

Question

In cases where there is a substantial difference in relative class frequencies, it could be that the density of the minority class is never higher than the density of the majority class anywhere in the attribute space. Here is a simple example using univariate Gaussian classes, with an imbalance ratio of 1:9.

In this case, if my classifier assigns all patterns to the majority class, it is doing exactly the right thing, and there is no problem to solve.

In this case, we know the true data generating process, so we know that the classifier is doing the right thing. However in general we don't know the true distributions of positive and negative classes, so we don't know whether the classifier is doing the right thing or not.

So my question is: In practical applications, how do we decide if we have a class imbalance problem, or whether the classifier is just giving the correct answer, to the question as posed?

Full disclosure: My intuition is that in most cases, especially when the data is not unduly scarce, the classifier is doing exactly what it should do and there is no class imbalance problem. I am primarily interested to hear how other practitioners and researchers diagnose class imbalance problems.

Answer 1

I challenge that there is a problem. Let's go with the scenario you described in the comments where your red graph is shifted to the right a bit.

I will make up some (plausible) numbers and go through Bayes' theorem.

$$ P(\text{red}) = 0.2$$$$P(\text{blue}) = 0.8 $$

$$ P(X>3\vert \text{red}) = 0.6$$$$P(X>3\vert \text{blue}) = 0.05 $$

Now Bayes' theorem:

$$ P(\text{red}\vert X>3) = \dfrac{P(X>3\vert\text{red})P(\text{red})}{P(X>3)} $$

$$P(X>3) = P(X>3\cap\text{red}) + P(X>3\cap\text{red}^C) $$$$= P(X>3\cap\text{red}) + P(X>3\cap\text{blue})$$ $$ = P(X>3\vert \text{red})P(\text{red}) + P(X>3\vert \text{blue})P(\text{blue}) $$$$=(0.6)(0.2) + (0.05)(0.8) = 0.16$$

Now let's put it all together in Bayes' theorem.

$$ P(\text{red}\vert X>3) = \dfrac{(0.6)(0.2)}{(0.16)} = 0.75 $$

That's a much larger probability of being red than the prior probability of $0.2$.

Varying the prior probability of being red reveals a similar story of consistently having a higher posterior probability of being red than prior probability of being red.

posterior <- function(x, y, z){
    return(x*y/(x*y + z*(1-x)))
}
prior <- seq(0, 1, 0.0001)
plot(prior, posterior(prior, 0.6, 0.05), xlab = "Prior of Red", ylab = "Posterior of Red", col = 'red')
lines(prior, prior)

The class imbalance does not overwhelm the posterior probability, and I have tried this with even smaller shifts of red to the right. A tiny shift results in a plot that is very close to the diagonal, but it still bends up a little bit.

Answer 2

I'm going to have a go at explaining why I think detecting a class imbalance problem is likely to be difficult because of the paucity of data when we actually do have a problem.

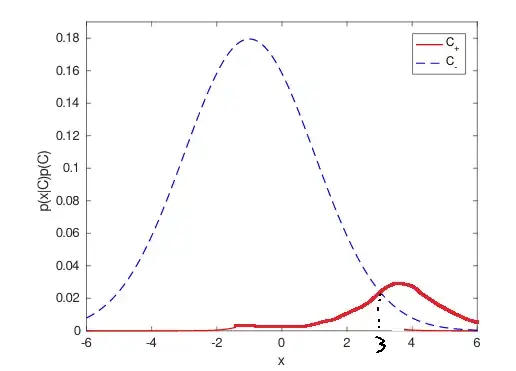
Consider a univariate normal pattern recognition task, with a 19:1 ratio of negative to positive examples (so that classifying everything as negative gives an accuracy of 95%), but where a decision boundary could be drawn giving an accuracy better than 95%. The ideal distributions and decision boundary are shown below:

The generalisation performance of the ideal classifier is as follows:

• TPR = 0.318385
• FNR = 0.681615
• TNR = 0.993286
• FPR = 0.006714
• ERR = 0.040459
• ACC = 0.959541

where TPR is the true positive rate, FNR is the false negative rate, TNR is the true negative rate, FPR is the false positive rate, ERR is the error rate and ACC = 1 - ERR is the accuracy.

Assume the variances of both classes are know, so we only need to estimate the class means. Unfortunately, if we have to estimate the means from only a small sample of data, we might be unlucky and end up with a model where the decision boundary is so far from areas of high data density that we may as well classify everything as belonging to the majority negative class. This is an example of the class imbalance problem, because the uncertainty in estimating the parameters leads to a bias against the minority positive class. Here we have a model with 152 negative patterns and 8 positive patterns:

I didn't have to work to hard to be unlucky, this is only the 21st seed of the random number generator I tried. The training set statistics are:

• TPR = 0.00
• FNR = 1.00
• TNR = 1.00
• FPR = 0.00
• ERR = 0.05
• ACC = 0.95

Clearly this is not very good, it is no better than classifying everything as negative.

So lets see if we can detect this problem by having a validation set, again with 152 negative examples and 8 positive examples, in the same ratio as the training set:

• TPR = 0.00
• FNR = 1.00
• TNR = 1.00
• FPR = 0.00
• ERR = 0.05
• ACC = 0.95

Oh dear, the validations set suggests this is a case where no meaningful classification is possible. However, we know that is not true in this case, by construction. The problem is that, like the training set, it is only a small sample of data, and we have just been unlucky again. If we were to sample some more validation data, we might get a different result. However, if we could collect more data, we would use it for training the model and we would get better parameter estimates and the class imbalance problem would likely go away.

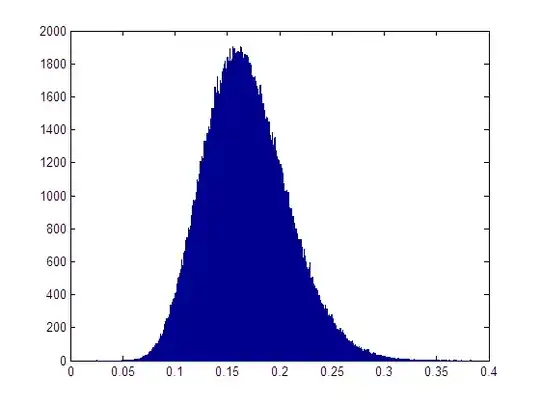
So my initial thought was to see if we could make a Bayesian test of whether it was plausible that there may be a non-trivial decision to be made, given the training data we actually have. If we choose an improper flat prior,our posterior distribution for the class means are Gaussian distributions, centered on the sample means, with standard deviations given by the standard errors of the means (in agreement with the frequentist confidence intervals). We can then perform a Monte Carlo simulation, of say 2^20 samples (as they can be collected so cheaply in this case and I like round numbers), and estimate the posterior distribution for the decision boundary.

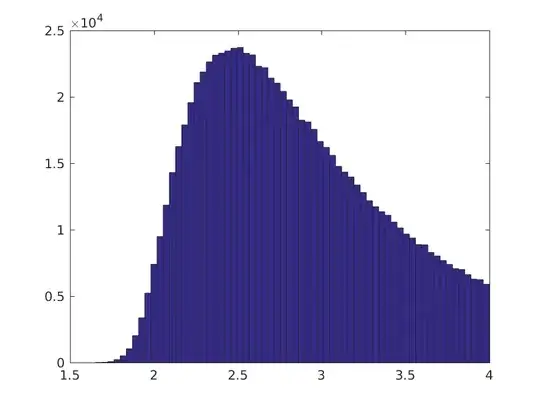
About 79% of the 2^20 samples gives a threshold that is in an area of high data density, the remaining 21% are so far to the right of both classes that essentially all patterns will be classified as negative. We can also look at the posterior distribution for the true positive rate:

This suggests that there is some chance of a meaningful classification. Let's make an arbitrary threshold at which we might consider a true positive rate as "meaningful" at 0.05. The proportion of Monte Carlo samples, for which the TPR >= 0.05 is about 22.7%, so in this case, we might diagnose the plausibility of a class imbalance problem.

However, what happens if we try it again, but this time for a problem where classifying everything as negative is more or less optimal:

where the optimal model's generalisation performance is summarised by:

• TPR = 0.007254
• FNR = 0.992746
• TNR = 0.999714
• FPR = 0.000286
• ERR = 0.049909
• ACC = 0.950091

Again we have to estimate the class means from a small dataset with 152 negative examples and 8 positive examples, and again we are unlucky,

The training set performance is given by:

• TPR = 0.25
• FNR = 0.75
• TNR = 1.00
• FPR = 0.00
• ERR = 0.0375
• ACC = 0.9625

and the validation set performance by

• TPR = 0.125
• FNR = 0.875
• TNR = 1.000
• FPR = 0.000
• ERR = 0.04375
• ACC = 0.95625

In this case, the Monte Carlo simulation is very confident that a meaningful classification is plausible

The proportion of Monte Carlo samples giving a TPR >= 0.05 is about 74.5%, when of course we know by construction that the optimal model assigns all patterns to the negative class.

This suggests the Bayesian analysis can suggest that a meaningful classification is plausible, even though we have a classifier that ostensibly classifies all patterns to the negative class. In that situation, we may want to think of doing something to alleviate the problem. However, such a test can't tell us when we should be classifying everything as negative.

Anyway, that was the sort of answer I was hoping for, but I'd much prefer something that actually worked in practice! ;o) I may well offer a second bounty if someone can provide something substantially better than this.

Answer 3

Well, I think the lack of an answer that explains how to detect whether class imbalance is a problem in a particular application, even when a modest bounty of +50 reputation was on offer, suggests cause for concern about research on the topic of class imbalance. I suspect practitioners are frequently re-balancing or re-weighting the datasets simply because they are imbalanced, rather than because the imbalance is actually causing a problem. I further suspect that often this is just making matters worse by over-compensating (e.g. by fully balancing the dataset).

Class imbalance can cause a problem when there are two few examples of the minority class to adequately characterise it's statistical distribution. When this happens, the decision boundary does tend to be unduly biased in favour of the majority class. However, as you add more data, the problem goes away. This shouldn't be a surprise. If you have a large enough neural network, it will be a universal approximator, able to implement essentially any (one-to-one or many-to-one) mapping between the input and output spaces. If it is fitted using a proper scoring rule then asymptotically it will output the true posterior probabilities of class membership. So if you have enough data, it doesn't matter how imbalanced the problem is, a complex enough model will learn the optimal decision surface.

I think any means of detecting and dealing with class imbalance problems will be very tricky though. Essentially if there is a bias, you will want to re-sample or re-weight the training sample just the right amount to compensate for the bias due to the "imbalance". Exactly balancing the dataset is likely to way over-compensate and make accuracy (or expected loss) worse rather than better. The trouble is, if you don't have enough data to describe the minority class, where are you going to get the data to choose the optimal degree of bias? I suspect the best approach will be some Bayesian scheme that determines what the plausible true positive rate (for example) could be if the model were correct.

Essentially, I know from experience that class imbalance can cause estimation problems, in a small data setting, but I'm not convinced that there is a great deal we can do about it because we don't have enough independent data to tune the compensation applied. I think we should be very wary of up/down sampling or reweighting simply because there is an imbalance, and if we do, we need to be able to determine whether it has worked or not. This requires at least that we know what criterion is important for our application, and why it is important. No application is primarily interested in the true positive rate, if that were true, we would just assign everything to the positive class and go home satisfied with having done the optimal job! ;o)