An alternative is the approach of Kooperberg and colleagues, based on estimating the density using splines to approximate the log-density of the data. I'll show an example using the data from @whuber's answer, which will allow for a comparison of approaches.
set.seed(17)
x <- rexp(1000)
You'll need the logspline package installed for this; install it if it is not:
install.packages("logspline")
Load the package and estimate the density using the logspline() function:
require("logspline")
m <- logspline(x)
In the following, I assume that the object d from @whuber's answer is present in the workspace.
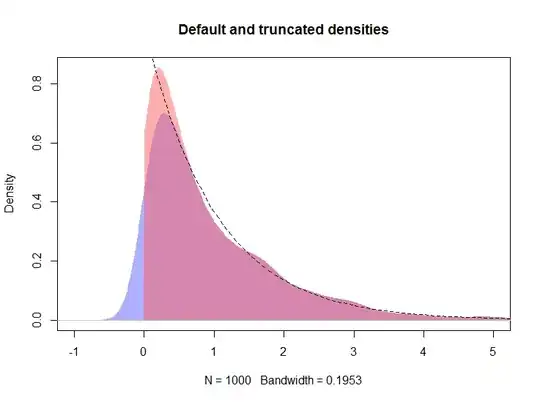
plot(d, type="n", main="Default, truncated, and logspline densities",
xlim=c(-1, 5), ylim = c(0, 1))
polygon(density(x, kernel="gaussian", bw=h), col="#6060ff80", border=NA)
polygon(d, col="#ff606080", border=NA)
plot(m, add = TRUE, col = "red", lwd = 3, xlim = c(-0.001, max(x)))
curve(exp(-x), from=0, to=max(x), lty=2, add=TRUE)
rug(x, side = 3)
The resulting plot is shown below, with the logspline density shown by the red line

Additionally, the support for the density can be specified via arguments lbound and ubound. If we wish to assume that the density is 0 to the left of 0 and there is a discontinuity at 0, we could use lbound = 0 in the call to logspline(), for example
m2 <- logspline(x, lbound = 0)
Yielding the following density estimate (shown here with the original m logspline fit as the previous figure was already getting busy).
plot.new()
plot.window(xlim = c(-1, max(x)), ylim = c(0, 1.2))
title(main = "Logspline densities with & without a lower bound",
ylab = "Density", xlab = "x")
plot(m, col = "red", xlim = c(0, max(x)), lwd = 3, add = TRUE)
plot(m2, col = "blue", xlim = c(0, max(x)), lwd = 2, add = TRUE)
curve(exp(-x), from=0, to=max(x), lty=2, add=TRUE)
rug(x, side = 3)
axis(1)
axis(2)
box()
The resulting plot is shown below
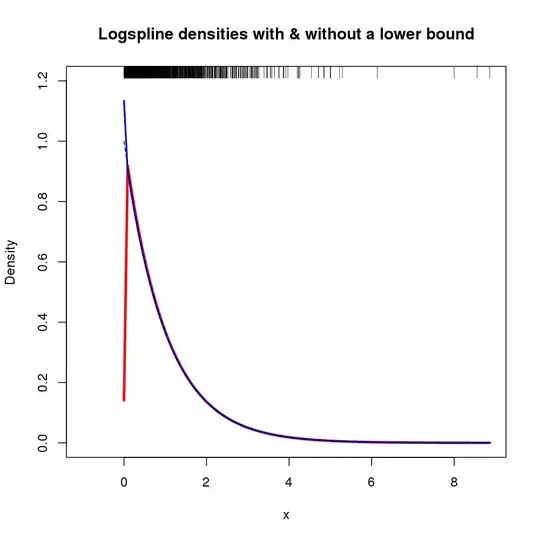
In this case, exploiting knowledge of x results in a density estimate that doesn't tend to 0 at $x = 0$, but is similar to the standard logspline fit elsewhere over x