1

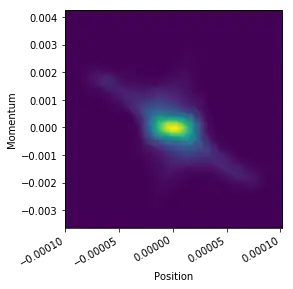
I am trying to estimate the PDF of the radius of points distributed in a 2D plane. The points are distributed like this:

enter image description here

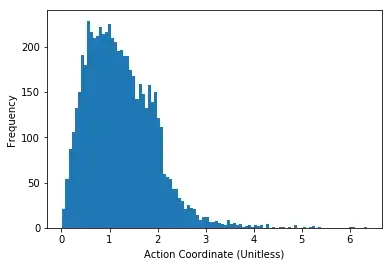
I can produce a histogram of the radius data which looks like this:

Histogram

I want to use kernel density estimation to produce a better result for the radial PDF and then get the value of the derivative of the PDF at $r=0$, but I immediately run into the problem that KDE will produce non-zero probability density for negative values of the radius. Is there a simple way to use KDE for this application? Maybe with an adaptive kernel? Any help would be greatly appreciated.

ElectronsAndStuff
  • 41
  • 4
  • 2
    One set of solutions is available at https://stats.stackexchange.com/questions/65866. However, the special nature of your problem provides other solutions, such as estimating the density of $r$ from (any) density estimate of $(x,y).$ Because the latter approach will produce no density for negative numbers, why not just use that? BTW, the physical meaning of $r$ is doubtful, because it will change depending on the units of position and momentum you use. – whuber Jan 13 '19 at 23:01

0 Answers0