I say 'mode' in the title – perhaps there's something more appropriate I can find. Here's my problem:
A person is in a $100\mathrm m$ by $500\mathrm m$ space.
I have about 100 samples randomly distributed in that space. Each sample is the relative probability that the person is at that point.
Here's very roughly what it looks like, where $\color{blue}{\textbf{X}}$ is the person, $\color{blue}\blacktriangle$ is my current prediction, and the dots represent a sample, with the relative probability represented by how dark it is.
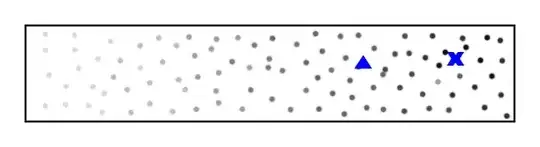
If they're at one end of the space, the samples nearest them might be ~0.1. The samples down the other end of the space might be ~0.001.
I'm currently locating them by taking the mean of the sample positions weighted according to their probability – i.e. the expected position.
That however performs very poorly particularly at the ends of the space – the sum of the low probabilities down the other end of the space weigh the weighted mean towards the opposite end to where they actually are. The result is that the estimation is rather biased towards the middle.
What can I do to get a more usable prediction, that isn't so heavily weighted towards the middle?
I've considered two things: kernel density estimation; and taking a power of the weights to more favour the higher probabilities. The former I think may not be an option due to highly constrained CPU in our use case (think near-real time on a pretty fast embedded device, while it's also doing other stuff); the latter I have yet to try out, though I'm not expecting particularly great results. I've read about mean shift after checking out this similar question, but I'm unsure how well it will perform with my use case, and I have no idea if it's computationally cheap enough (I have yet to quite get my head around how it works).
Something else I should mention, the samples are randomly distributed at the very beginning – given their positions we can pre-compute however much we want, it's only estimating the position given the sample data that is CPU-constrained.