John Fox's book An R companion to applied regression is an excellent ressource on applied regression modelling with R. The package car which I use throughout in this answer is the accompanying package. The book also has as website with additional chapters.
Transforming the response (aka dependent variable, outcome)
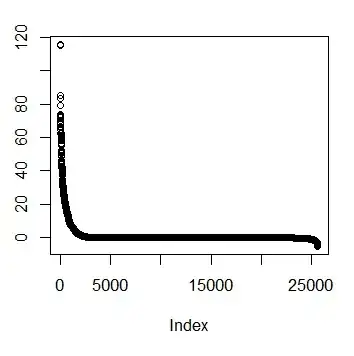
Box-Cox transformations offer a possible way for choosing a transformation of the response. After fitting your regression model containing untransformed variables with the R function lm, you can use the function boxCox from the car package to estimate $\lambda$ (i.e. the power parameter) by maximum likelihood. Because your dependent variable isn't strictly positive, Box-Cox transformations will not work and you have to specify the option family="yjPower" to use the Yeo-Johnson transformations (see the original paper here and this related post):
boxCox(my.regression.model, family="yjPower", plotit = TRUE)
This produces a plot like the following one:
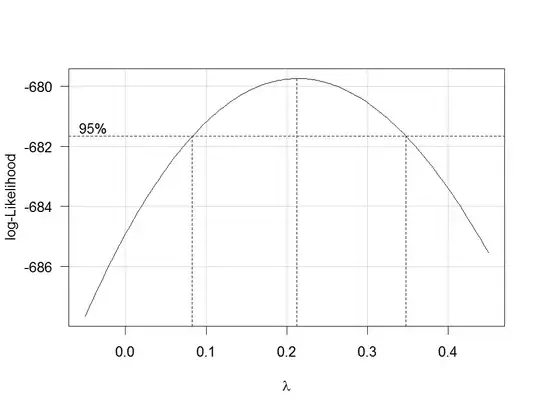
The best estimate of $\lambda$ is the value that maximizes the profile likelhod which in this example is about 0.2. Usually, the estimate of $\lambda$ is rounded to a familiar value that is still within the 95%-confidence interval, such as -1, -1/2, 0, 1/3, 1/2, 1 or 2.
To transform your dependent variable now, use the function yjPower from the car package:
depvar.transformed <- yjPower(my.dependent.variable, lambda)
In the function, the lambda should be the rounded $\lambda$ you have found before using boxCox. Then fit the regression again with the transformed dependent variable.
Important: Rather than just log-transform the dependent variable, you should consider to fit a GLM with a log-link. Here are some references that provide further information: first, second, third. To do this in R, use glm:
glm.mod <- glm(y~x1+x2, family=gaussian(link="log"))
where y is your dependent variable and x1, x2 etc. are your independent variables.
Transformations of predictors
Transformations of strictly positive predictors can be estimated by maximum likelihood after the transformation of the dependent variable. To do so, use the function boxTidwell from the car package (for the original paper see here). Use it like that: boxTidwell(y~x1+x2, other.x=~x3+x4). The important thing here is that option other.x indicates the terms of the regression that are not to be transformed. This would be all your categorical variables. The function produces an output of the following form:
boxTidwell(prestige ~ income + education, other.x=~ type + poly(women, 2), data=Prestige)
Score Statistic p-value MLE of lambda
income -4.482406 0.0000074 -0.3476283
education 0.216991 0.8282154 1.2538274
In that case, the score test suggests that the variable income should be transformed. The maximum likelihood estimates of $\lambda$ for income is -0.348. This could be rounded to -0.5 which is analogous to the transformation $\text{income}_{new}=1/\sqrt{\text{income}_{old}}$.
Another very interesting post on the site about the transformation of the independent variables is this one.
Disadvantages of transformations
While log-transformed dependent and/or independent variables can be interpreted relatively easy, the interpretation of other, more complicated transformations is less intuitive (for me at least). How would you, for example, interpret the regression coefficients after the dependent variables has been transformed by $1/\sqrt{y}$? There are quite a few posts on this site that deal exactly with that question: first, second, third, fourth. If you use the $\lambda$ from Box-Cox directly, without rounding (e.g. $\lambda$=-0.382), it is even more difficult to interpret the regression coefficients.
Modelling nonlinear relationships
Two quite flexible methods to fit nonlinear relationships are fractional polynomials and splines. These three papers offer a very good introduction to both methods: First, second and third. There is also a whole book about fractional polynomials and R. The R package mfp implements multivariable fractional polynomials. This presentation might be informative regarding fractional polynomials. To fit splines, you can use the function gam (generalized additive models, see here for an excellent introduction with R) from the package mgcv or the functions ns (natural cubic splines) and bs (cubic B-splines) from the package splines (see here for an example of the usage of these functions). Using gam you can specify which predictors you want to fit using splines using the s() function:
my.gam <- gam(y~s(x1) + x2, family=gaussian())
here, x1 would be fitted using a spline and x2 linearly as in a normal linear regression. Inside gam you can specify the distribution family and the link function as in glm. So to fit a model with a log-link function, you can specify the option family=gaussian(link="log") in gam as in glm.
Have a look at this post from the site.