6

I want to train a linear regression model to predict a non-linear variable. This how the two independent variables correlated against the response (points are jittered):

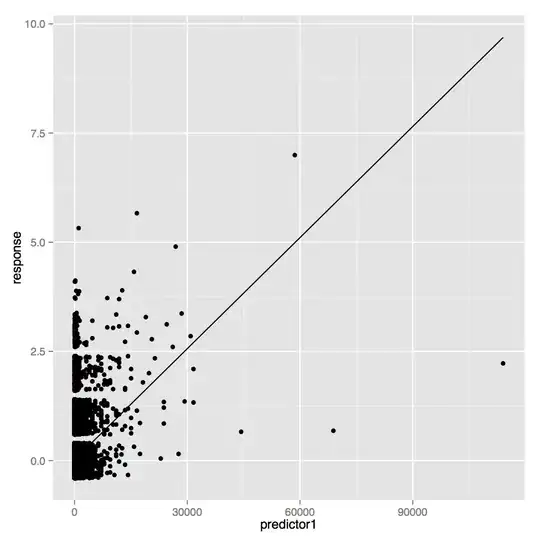
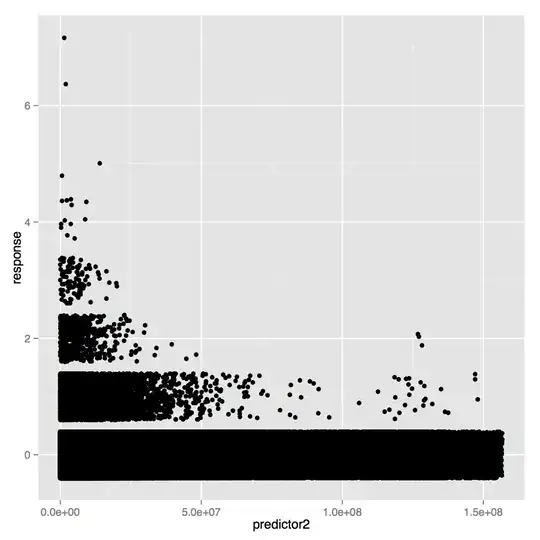
enter image description here

enter image description here

And the residuals against the fitted values:

enter image description here

Most of the values for the response are zero. The effect is a very strong heteroscedasticity

        studentized Breusch-Pagan test

data:  model
BP = 55483.84, df = 2, p-value < 2.2e-16

event though the the predictors are strongly correlated with the response

Call:
lm(formula = response ~ predictor1 + predictor2, data = train_predictors)

Residuals:
    Min      1Q  Median      3Q     Max 
-7.6996 -0.0268 -0.0238 -0.0182  4.8785 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept)  2.748e-02  2.825e-04   97.28   <2e-16 ***
predictor1   8.491e-05  6.574e-07  129.16   <2e-16 ***
predictor2  -3.934e-10  8.298e-12  -47.41   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.1561 on 498498 degrees of freedom
Multiple R-squared:  0.0365,    Adjusted R-squared:  0.0365 
F-statistic:  9442 on 2 and 498498 DF,  p-value: < 2.2e-16

Should I consider more adopting non-linear models or could I first try correcting the non-linearity of the response?

Community
  • 1
Francesco
  • 713
  • 6
  • 17
  • 3
    "Linearity" (or lack thereof) refers to the relationship between the predictors and the response, about which you have offered no direct relevant information. Could you please amend your post to provide that? – whuber Mar 05 '14 at 02:36
  • 5
    In addition to @whuber's point, the marginal distribution of the response is not really of interest, but rather the conditional distribution / the distribution of the residuals. On another note, are all Y values integers / counts? – gung - Reinstate Monica Mar 05 '14 at 02:38
  • 1
    Some useful searches you can investigate include [multinomial logistic regression](http://stats.stackexchange.com/search?q=multinomial+logistic+regression) and [ordinal regression](http://stats.stackexchange.com/search?q=ordinal+regression). – whuber Mar 05 '14 at 03:25
  • Is the response a *count* or does it represent some categorical thing, or something else? – Glen_b Jan 02 '15 at 02:45

1 Answers1

1

I don't know details of your model, but in my opinion you need to deal with the large amount of "zero responses". Look into compound models with a mass point at zero. Something like the "Tweedie model".

gung - Reinstate Monica
  • 132,789
  • 81
  • 357
  • 650
blew
  • 31
  • 2