9

EDIT: Since making this post, I have followed up with an additional post here.

Summary of the text below: I am working on a model and have tried linear regression, Box Cox transformations and GAM but have not made much progress

Using R, I am currently working on a model to predict the success of minor league baseball players at the major league (MLB) level. The dependent variable, offensive career wins above replacement (oWAR), is a proxy for success at the MLB level and is measured as the sum of offensive contributions for every play the player is involved in over the course of his career (details here - http://www.fangraphs.com/library/misc/war/). The independent variables are z-scored minor league offensive variables for statistics that are thought to be important predictors of success at the major league level including age (players with more success at a younger age tend to be better prospects), strike out rate [SOPct], walk rate [BBrate] and adjusted production (a global measure of offensive production). Additionally, since there are multiple levels of the minor leagues, I have included dummy variables for the minor league level of play (Double A, High A, Low A, Rookie and Short Season with Triple A [the highest level before the major leagues] as the reference variable]). Note: I have re-scaled WAR to to be a variable that goes from 0 to 1.

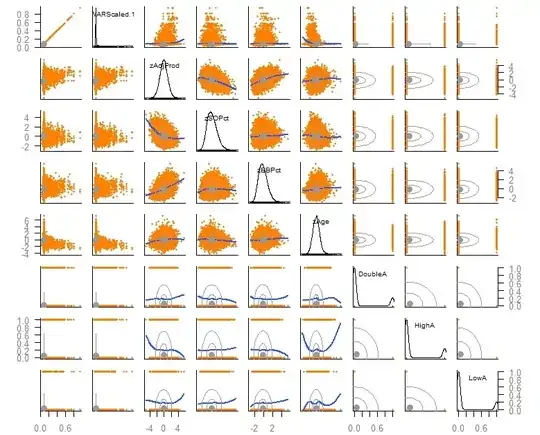
The variable scatterplot is as follows:

scatterplot

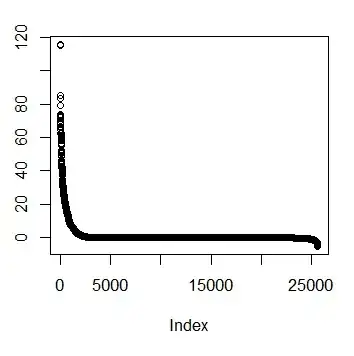
For reference, the dependent variable, oWAR, has the following plot:

dependentvariableplot

I started with a linear regression oWAR = B1zAge + B2zSOPct + B3zBBPct + B4zAdjProd + B5DoubleA + B6HighA + B7LowA + B8Rookie + B9ShortSeason and obtained the following diagnostics plots:

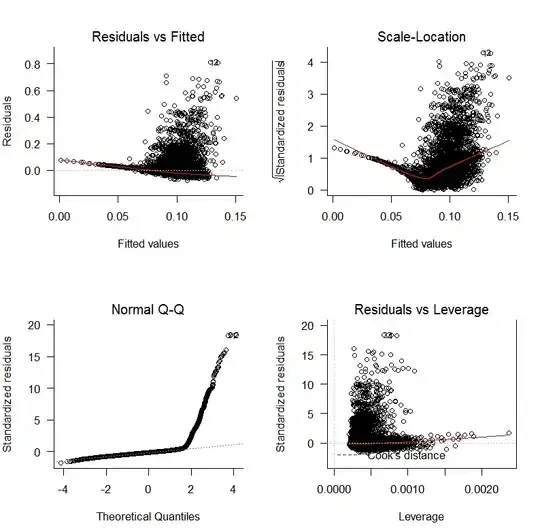
linearRegressionDiagnostics

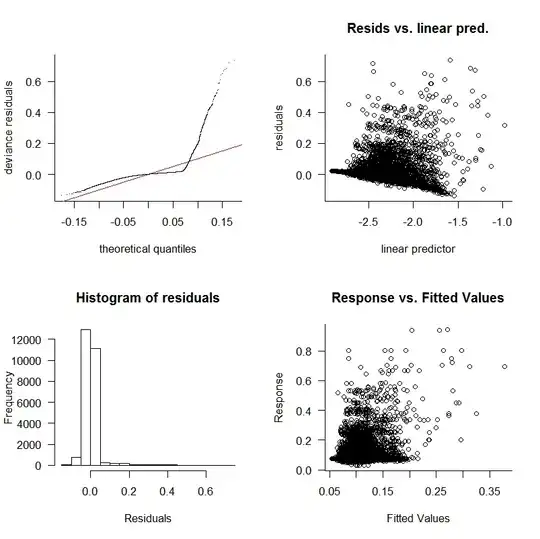
There are clear problems with a lack of unbiasedness of the residuals and a lack of random variation. Additionally, the residuals are not normal. The results of the regression are shown below:

linearRegressionResults

Following the advice in a previous thread, I tried a Box-Cox transformation with no success. Next, I tried a GAM with a log link and received these plots:

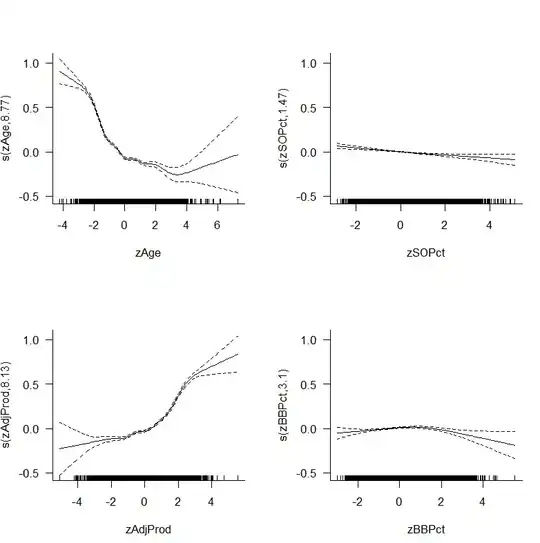
splines

Original diagnosticChecksGAM

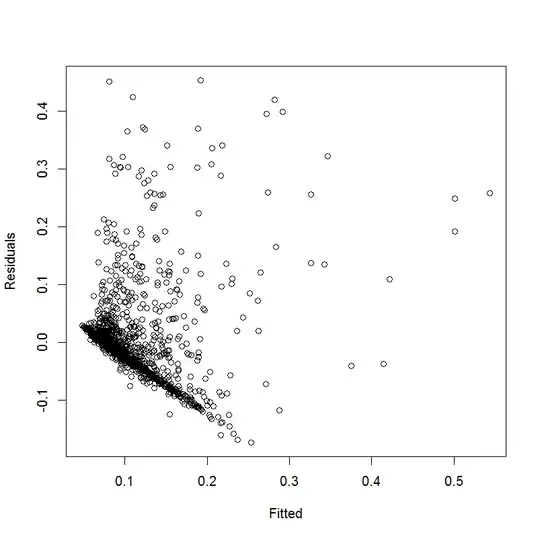
New Diagnostic Plot GAMDiag

It looks like the splines helped fit the data but the diagnostic plots still show a poor fit. EDIT: I thought I was looking at the residuals vs fitted values originally but I was incorrect. The plot that was originally shown is marked as Original (above) and the plot I uploaded afterwards is marked as New Diagnostic Plot (also above)

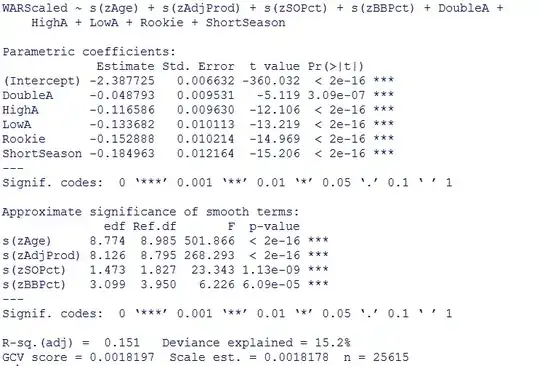
GAMResults

The $R^2$ of the model has increased

but the results produced by the command gam.check(myregression, k.rep = 1000) are not that promising.

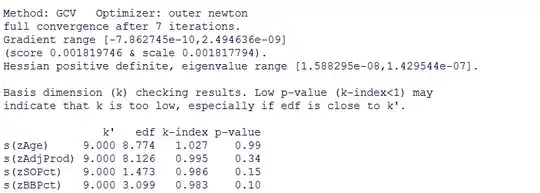
GAMResults2

Can anyone suggest a next step for this model? I am happy to provide any other information that you think might be useful to understand the progress I've made thus far. Thanks for any help you can provide.

Community
  • 1
zgall1
  • 809
  • 2
  • 13
  • 17
  • 2
    I found the code in this excellent primer on GAM in R - http://www3.nd.edu/~mclark19/learn/GAMS.pdf The code: library(car) scatterplotMatrix(mydata[,c(1,1:8)],pch=19,cex=.5,reg.line=F, lwd.smooth=1.25, spread=F,ellipse=T, col=c('gray60','#2957FF','#FF8000'), col.axis='gray50') – zgall1 Jun 12 '13 at 14:05
  • 1
    Can you share your dataset? Also, +1 for that scatterplot matrix. It's excellent. – Zach Jun 12 '13 at 14:10
  • @Zach I've been asked to refrain from sharing the entire dataset but I am happy to share any additional plots that might provide insight. – zgall1 Jun 12 '13 at 14:12
  • 1
    That's too bad, it looks like an interesting dataset. My suggestion would be to try some other machine learning algorithms, e.g. a random forest. – Zach Jun 12 '13 at 14:24
  • @Zach Is a random forest a type of neural network? – zgall1 Jun 12 '13 at 14:39
  • 2
    Random forests are based on decision trees. Check out the randomForest package in R, and the random forest wikipedia page: http://en.wikipedia.org/wiki/Random_forest – Zach Jun 12 '13 at 14:47
  • 2
    "The dependent variable...is measured as the sum of offensive contributions for every play the player is involved in over the course of his career." This jumps out to me. A serious confounder here is how long a player has been playing, both in that [a] longer playtime means more time to "collect" oWAR [b] better players will probably play for longer periods of time. – Affine Jun 13 '13 at 14:00
  • Dealing with that will probably help considerably. However, I'm not sure what the best way here is. I don't think sticking playtime as a variable will completely solve the problem, given problem [b] (you won't have clean identification). – Affine Jun 13 '13 at 14:06
  • Problem a is not really a problem because all of these players' careeers are over. Problem b is potentially interesting but if better players play for longer, I'm not sure how that is a problem. In a sense, we are hoping that the data can predict who will play for a longer period of time. – zgall1 Jun 13 '13 at 20:21
  • Why do you think the output of `gam.check()` is not promising? Non of the p-values indicates significant pattern related to too-low dimensionality in the basis functions used. – Gavin Simpson Jun 14 '13 at 02:36
  • Not quite what I meant with [a]. An example might clarify what I meant. Let's say I wanted to look at the mileage driven on cars. I'd expect that the age of the car would be a very strong predictor simply since older cars have had the *time* to be driven more. Similarly here. Of course, you have the issue here where time played simply *cannot* be a variable because of "data leakage" and since you would have no idea how long a player will play for at the time you want to make a prediction. More later. – Affine Jun 14 '13 at 04:26
  • @GavinSimpson I was referring the biasedness, lack of random variation and non-normality of the residuals. – zgall1 Jun 14 '13 at 13:00
  • 1
    @zgall1 You mean in the plot (not shown?) – Gavin Simpson Jun 14 '13 at 15:10
  • @GavinSimpson I just realized I was misreading the plot I showed. Let me actually calculate a plot of residuals vs fitted values. – zgall1 Jun 14 '13 at 17:14
  • @GavinSimpson I uploaded the correct residuals vs fitted values. There still appears to be issues. Would you agree? – zgall1 Jun 14 '13 at 17:30
  • @zgall1 Well yes, but you've only fitted a Gaussian model here and the error distribution for these data/model is not Gaussian. If the response is a count you need something to handle that - hence the ZINB you fitted in the other post. If the response is a count scaled by some other value then put that other value in as a offset term. To get to a ZINB with smooths you either need to create the basis functions yourself using the splines package and add them to the model formula in `zeroinfl()` (or as Frank said below) or you're getting into the territory of BUGS/JAGS. Or possibly pkg gamlss... – Gavin Simpson Jun 14 '13 at 17:41
  • @GavinSimpson I appreciate the comment but it is so far over my head I don't even know where to start. I have only a rudimentary stats background and this stuff, while very interesting, is a pretty big challenge for me to grasp. I'm going to run your ideas by someone I know who might be able to help me out. Once again, thank you for all the help you've provided thus far. – zgall1 Jun 14 '13 at 19:02

2 Answers2

6

Very nice work. I think this situation is a candidate for the proportional odds semiparametric ordinal logistic model. The lrm function in the R rms package will fit the model. For now you may want to round $Y$ to have only 100-200 levels. Soon a new version of rms will be released with a new function orm that efficiently allows for thousands of intercepts in the model, i.e., allows $Y$ to be fully continuous [update: this appeared in 2014]. The proportional odds model $\beta$s are invariant to how $Y$ is transformed. That means quantiles are invariant also. When you want a predicted mean, $Y$ is assumed to be on the proper interval scale.

Frank Harrell
  • 74,029
  • 5
  • 148
  • 322
  • 1
    By levels, do you mean binning the Y variable into 100-200 buckets? If so, is there any preferred method for choosing the bin size? Should they be equally sized? – zgall1 Jun 12 '13 at 14:20
  • 1
    Just do the binning temporarily unless we have the continuous solution. You can bin into 100 percentiles, e.g. `require(Hmisc); cut2(y, g=100, levels.mean=TRUE)` – Frank Harrell Jun 12 '13 at 22:45
  • When you say a new version of `rms` will be released soon, do you have any idea when that might be? – zgall1 Jun 13 '13 at 14:30
  • If you use linux I can give it to you now, otherwise expect 2 weeks. – Frank Harrell Jun 13 '13 at 15:10
  • I do not use Linux so I guess I'll have to wait. Please let me know when it is available. – zgall1 Jun 14 '13 at 12:59
1

I think re-working the dependent variable and model can be fruitful here. Looking at your residuals from the lm(), it seems that the major issue is with the players with a high career WAR (which you defined as sum of all WAR). Notice that your highest predicted (scaled) WAR is 0.15 out of a maximum of 1! I think there's two things with this dependent variable that is exacerbating this issue:

  • Players that simply play for longer have more time to collect WAR
  • Good players will tend to be kept around longer, and will thus have the opportunity to have that longer time to collect WAR

However in the context of prediction, including time played explicitly as a control (in any manner, whether as a weight, or as the denominator in calculating average career WAR) is counterproductive (also I suspect it's effect would also be non-linear). Thus I suggest modeling time somewhat less explicitly in a mixed model using lme4 or nlme.

Your dependent variable would be seasonal WAR, and you would have a different number $j=m_i$ of seasons per player $i$. The model would have player as a random effect, and would be along the lines of:

$ sWAR_{ij} = \alpha + \sigma^2_i + \text{<other stuff>} + \varepsilon_{ij}$

With lme4, this would look something like
lmer(sWAR ~ <other stuff> + (1|Player), data=mydata)

You still may need to transform on $sWAR$, but I think this will help out on that feedback loop.

Affine
  • 2,307
  • 19
  • 25
  • I'm not sure I fully understand. If the dependent variable is seasonal WAR, what are the independent variables? An identical minor league stat line for each player? Are we essentially saying that minor league stat line A can lead to major league WAR B, C, D and E? – zgall1 Jun 14 '13 at 12:46
  • Also, since posting this model, I have followed up with an additional post you may want to check out here: http://stats.stackexchange.com/questions/61711/fitting-a-zero-inflated-negative-binomial-regression-with-r – zgall1 Jun 14 '13 at 12:47