8

Both answers in these threads, one and two claim that $Y$ should be transformed before applying any other transformation to the predictors. Indeed Weisberg chapter on transformations focus more on DV than predictors, and so does the R car package powerTransform() manual page.

However, we know that normality of the DV distribution is not a requirement in OLS to estimate BLUE coefficients and, even when the residuals are not strictly normally distributed, OLS is still a reasonable estimator.

So why the emphasis on transforming $Y$? There are a couple of reasons I think it's actually preferable not to transform $Y$: first it makes the IVs relationship harder to read and second, in prediction, it requires a back-transform from the estimated value to the original $Y$ scale. Depending what you're doing this can be an issue.

Community
  • 1
Robert Kubrick
  • 4,078
  • 8
  • 38
  • 55
  • 2
    We've had generalised linear models in name since 1972 and in particular cases for much longer. That is, using appropriate link functions can give you all the advantages of using a non-linear scale with all the advantages of getting predictions on the scale of the original data. Why is this not more widely known and practised? Longer replies are needed and will be forthcoming but analysing nonlinear relationships with linear tools applied to untransformed data rarely works well. – Nick Cox Sep 23 '14 at 18:14
  • 1
    +1 to @Nick. Additionally, analyzing relationships with almost *any* standard procedure (i.e., based on nearly-Normal distributions) in circumstances where the error distribution is strongly skewed is usually complicated and unsatisfactory, too. Nonlinear re-expressions actually achieve three things (and often do them all simultaneously): they *symmetrize distributions* of residuals, create *homoscedasticity*, and *linearize relationships.* – whuber Sep 23 '14 at 18:23

2 Answers2

5

Transforming X doesn't impact the shape of the conditional distribution, nor heteroskedasticity, so transforming X really only serves to deal with nonlinear relationships. (If you're fitting additive models it might serve to help with eliminating interaction, but even that's often best left to transforming Y)

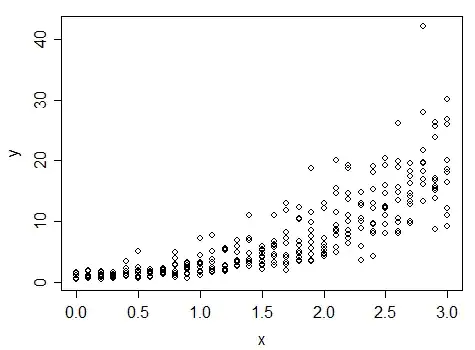
An example where transforming only X makes sense:
enter image description here

If that's - lack of fit in conditional mean - is your main issue, then transforming X may make sense, but if you're transforming because of the shape of the conditional Y or because of heteroskedasticity, if you're solving that by transformation (not necessarily the best choice, but we're taking transformation as a given for this question), then you must transform Y in some way to change it.

Consider, for example, a model where conditional variance is proportional to mean:

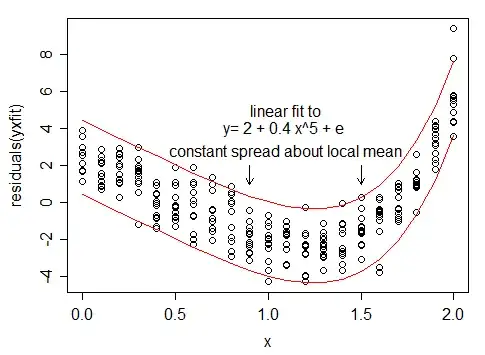
An example where transforming only X can't solve the problems:
enter image description here

Moving values on the x-axis won't change the fact that the spread is greater for values on the right than values on the left. If you want to fix this changing variance by transformation, you have to squish down high Y-values and stretch out low Y-values.

Now, if you're considering transforming Y, that will change the shape of the relationship between response and predictors ... so you'll often expect to transform X as well if you want a linear model (if it was linear before transforming, it won't be afterward). Sometimes (as in the second plot above), a Y=transformation will make the relationship more linear at the same time - but it's not always the case.

If you're transforming both X and Y, you want to do Y first, because of that change in the shape of the relationship between Y and X - usually you need to see what relationships are like after you transform. Subsequent transformation of X will then aim to obtain linearity of relationship.

So in general, if you're transforming at all, you often need to transform Y, and if you're doing that, you nearly always want to do it first.

Glen_b
  • 257,508
  • 32
  • 553
  • 939
  • If we have $Y = \beta{_0} + \beta{_1}X{^5} + \epsilon$ the residuals will have increasing variance regressing against $X{^1}$ (untransformed). Of course transforming $X$ has an impact on residuals heteroskedasticity. – Robert Kubrick Sep 24 '14 at 12:08
  • 1
    @RobertKubrick *not* relative to their local mean. See my edited post. – Glen_b Sep 24 '14 at 13:27
  • I still don't see it. I believe the variance changes are actually because of $\epsilon$, not $Y$ conditional distribution. Btw, the plot you posted is for the untransformed $X$. I know you did it to show the non-linearity of the relationship but it's a bit confusing in the context of your answer. – Robert Kubrick Sep 24 '14 at 14:13
  • $\text{Var}(\epsilon)=\text{Var}(Y|X)$. You seem to be distinguishing between the two variances, but they're not distinct. – Glen_b Sep 24 '14 at 14:34
  • True, they are the same. But mathematically we don't need to modify exponents on both sides of the equation to solve. You can verify this by running a simple boxcox estimator: after refining the $X$ exponent the solution for $Y$ will be 1. And transforming $X$ *does* change the residuals of the conditional distribution. – Robert Kubrick Sep 24 '14 at 14:51
  • 1
    It changes only the conditional mean. That's the point being made in my answer. – Glen_b Sep 24 '14 at 14:57
  • Let us [continue this discussion in chat](http://chat.stackexchange.com/rooms/17408/discussion-between-robert-kubrick-and-glen-b). – Robert Kubrick Sep 24 '14 at 16:04
2

Transforming Y initially is an anachronistic approach to data analysis. Our great-great-great grandfathers did that so why shouldn't we? Lots of reasons and your post reflecting that Gaussian assumptions are solely based on the errors from a model NOT the Y series is dead-on.

gung - Reinstate Monica
  • 132,789
  • 81
  • 357
  • 650
IrishStat
  • 27,906
  • 5
  • 29
  • 55
  • 4
    I agree with the first sentence more than I disagree; nevertheless the answer is more than a little over-simplified. Examples like pH or decibels show that scientific measurement is often already on a transformed scale, and with good reasons. Many economists routinely use log income not income as their response variable and that fits with the way that ordinary people make many decisions (e.g. in terms of percent thinking). (The history here is I think arguable too; transformations were not especially common before the middle 20th century.) – Nick Cox Sep 23 '14 at 18:22
  • @Nick I was speaking tongue-in-cheek about my forefathers . Transformations started to appear in the mid fifties ..... – IrishStat Sep 23 '14 at 18:47
  • 3
    Tongue-in-cheek and colourful exaggeration I readily buy, but nevertheless precise statements should be correct. Literature on the lognormal started in the 19th century, as did logarithmic graph paper. Transformations were the subject of several reviews before the 1950s, e.g. Bartlett's paper in _Biometrics_ 1947, so the literature is older. That's consistent, I think, with my earlier assertion about their being "not especially common". – Nick Cox Sep 23 '14 at 18:51
  • 3
    @Nick Scientists were using transformations long before 1947, because they are so natural. A nice case in point is Rydberg's derivation of his [formula for the hydrogen spectrum](http://en.wikipedia.org/wiki/Rydberg_formula#History), obtained in the 1880's by choosing suitable nonlinear transformations of the variables. One could appeal to [Fechner's work in psychophysics](http://en.wikipedia.org/wiki/Psychophysics#History) c. 1860, too. This practice is so effective and important in the sciences that one cannot take seriously the first statement in this answer that it is "anachronistic." – whuber Sep 23 '14 at 19:49
  • 3
    @whuber We agree, in essence. There is a spectrum (pun intended) from uses of transformations in physical and other sciences, often arising as a means of or as a consequence of discovering nonlinear relationships, to deliberate use of transformations of raw data as recommended by (some) statisticians. I wouldn't want to draw a line between the two, as that would be futile and not helpful. – Nick Cox Sep 23 '14 at 20:18