How to statistically compare two time series?

Question

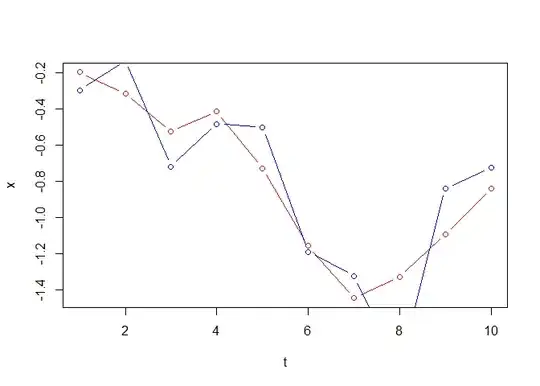
I have two time series, shown in the plot below:

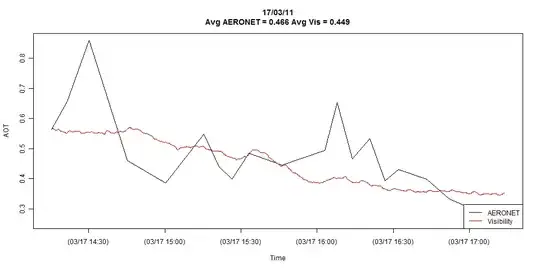
The plot is showing the full detail of both time series, but I can easily reduce it to just the coincident observations if needed.

My question is: What statistical methods can I use to assess the differences between the time series?

I know this is a fairly broad and vague question, but I can't seem to find much introductory material on this anywhere. As I can see it, there are two distinct things to assess:

1. Are the values the same?

2. Are the trends the same?

What sort of statistical tests would you suggest looking at to assess these questions? For question 1 I can obviously assess the means of the different datasets and look for significant differences in distributions, but is there a way of doing this that takes into account the time-series nature of the data?

For question 2 - is there something like the Mann-Kendall tests that looks for the similarity between two trends? I could do the Mann-Kendall test for both datasets and compare, but I don't know if that is a valid way to do things, or whether there is a better way?

I'm doing all of this in R, so if tests you suggest have a R package then please let me know.

Answer 1

As others have stated, you need to have a common frequency of measurement (i.e. the time between observations). With that in place I would identify a common model that would reasonably describe each series separately. This might be an ARIMA model or a multiply-trended Regression Model with possible Level Shifts or a composite model integrating both memory (ARIMA) and dummy variables. This common model could be estimated globally and separately for each of the two series and then one could construct an F test to test the hypothesis of a common set of parameters.

Answer 2

Consider the grangertest() in the lmtest library.

It is a test to see if one time series is useful in forecasting another.

A couple references to get you started:

https://spia.uga.edu/faculty_pages/monogan/teaching/ts/

https://spia.uga.edu/faculty_pages/monogan/teaching/ts/Kgranger.pdf

http://en.wikipedia.org/wiki/Granger_causality

Answer 3

Just came across this. Your first answer us plotting g the two sets the same scale (timewise) to see the differences visually. You have done this and can easily see there are some glaring differences. The next step is to use simple correlation analysis...and see how well are they related using the correlation coefficient (r). If the r is small your conclusion would be that they are weakly related and so no desirable comparisons and a larger value if r would suggest good comparisons s between the two series. The third step where there is good correlation is to test the statistical significance of the r. Here you can use the Shapiro Welch test which would assume the two series are normally distributed (null hypothesis ) or not (alternative hypothesis). There are other tests you can do but let me hope my answer helps.

Answer 4

I want to propose another approach. This is to test whether two time series are the same. This approach is only suitable for infrequently sampled data where autocorrelation is low.

If time series x is the similar to time series y then the variance of x-y should be less than the variance of x. We can test this using a one sided F test for variance. If the ratio var(x-y)/var(x) is significantly less than one then then y explains a significant proportion of the variance of x.

We also need to check that x-y is not significantly different to 0. This can be done with a one sample two sided t.test.

x <- cumsum(runif(10)-0.5)
t <- seq_along(x)
y <- x + rnorm(10, 0, 0.2)
# y <- x + rnorm(10, 0.2, 0.2)
plot(t,x, "b", col = "red")
points(t,y, "b", col = "blue")

var.test(x-y, x, alternative = "less") # does y improve variance of x?
#> 
#>  F test to compare two variances
#> 
#> data:  x - y and x
#> F = 0.27768, num df = 9, denom df = 9, p-value = 0.03496
#> alternative hypothesis: true ratio of variances is less than 1
#> 95 percent confidence interval:
#>  0.0000000 0.8827118
#> sample estimates:
#> ratio of variances 
#>           0.277679
t.test(x-y) # check that x-y does not have an offset
#> 
#>  One Sample t-test
#> 
#> data:  x - y
#> t = -0.0098369, df = 9, p-value = 0.9924
#> alternative hypothesis: true mean is not equal to 0
#> 95 percent confidence interval:
#>  -0.1660619  0.1646239
#> sample estimates:
#>     mean of x 
#> -0.0007189834

^{Created on 2021-09-02 by the reprex package (v2.0.0)}

I think it should be possible to extend this approach to test whether two time series are linearly correlated, using x-lm(x ~ y) instead of x-y.

Edit: Dealing with autocorrelation I think could be done by finding a suitable Effective Degrees of Freedom for the tests, c.f., https://doi.org/10.1016/j.neuroimage.2019.05.011

Answer 5

Fit a straight line to both the time series signals using polyfit. Then compute root-mean-square-error (RMSE) for both the lines. The obtained value for the red-line would be quite less than the one obtained for gray line.

Also make the readings on some common frequency.