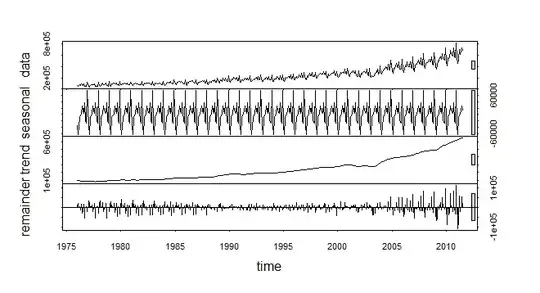
With the below dataset, I have a series which needs transforming. Easy enough. However, how do you decide which of the SQRT or LOG transformations is better? And how do you draw that conclusion?
x<-c(75800,54700,85000,74600,103900,82000,77000,103600,62900,60700,58800,134800,81200,47700,76200,81900,95400,85400,84400,103400,63000,65500,59200,128000,74400,57100,75600,88300,111100,95000,91500,111400,73700,72800,64900,146300,83100,66200,101700,100100,120100,100200,97000,120600,88400,83500,73200,141800,87700,82700,106000,103900,121000,98800,96900,115400,87500,86500,81800,135300,88900,77100,109000,104000,113000,99000,104500,109400,92900,88700,90500,140200,91700,78800,114700,100700,113300,122800,117900,122200,102900,85300,92800,143800,88400,75400,111200,96300,114600,108300,113400,116600,103400,87300,88200,149800,90100,78800,108900,126300,122000,125100,119600,148800,114600,101600,108800,174100,101100,89900,126800,126400,141400,144700,132800,149000,124200,101500,106100,168100,104200,79900,126100,121600,139500,143100,144100,154500,129500,109800,116200,171100,106700,85500,132500,133700,135600,149400,157700,144500,165400,122700,113700,175000,113200,94400,138600,132400,129200,165700,153300,141900,170300,127800,124100,206700,131700,112700,170900,153000,146700,197800,173800,165400,201700,147000,144200,244900,146700,124400,168600,193400,167900,209800,198400,184300,214300,156200,154900,251200,127900,125100,171500,167000,163900,200900,188900,168000,203100,169800,171900,241300,141400,140600,172200,192900,178700,204600,222900,179900,229900,173100,174600,265400,147600,140800,171900,189900,185100,218400,207100,178800,228800,176900,170300,251500,149900,150300,192000,185100,184500,228800,219000,180000,241500,184300,174600,264500,166100,151900,194600,214600,201700,229400,233600,197500,254600,194000,201100,279500,175800,167200,235900,207400,215900,261800,236800,222400,281500,214100,218200,295000,194400,180200,250400,212700,251300,280200,249300,240000,304200,236900,232500,300700,207300,196900,246600,262500,272800,282300,271100,265600,313500,268000,256500,318100,232700,198500,268900,244300,262400,289200,286600,281100,330700,262000,244300,309300,246900,211800,263100,307700,284900,303800,296900,290400,356200,283700,274500,378300,263100,226900,283800,299900,296000,327600,313500,291700,333000,246500,227400,333200,239500,218600,283500,267900,294500,318600,318700,283400,351600,268400,251100,365100,249100,216400,245500,232100,236300,275600,296500,296900,354300,277900,287200,420200,299700,268200,329700,353600,356200,396500,379500,349100,437900,350600,338600,509100,342300,288800,378400,371200,395800,450000,414100,387600,486600,355300,358800,526800,346300,295600,361500,415300,402900,484100,412700,395800,491300,391000,374900,569200,369500,314900,422500,436400,439700,509200,461700,449500,560600,435000,429900,633400,417900,365700,459200,466500,488500,531500,483500,485400,575700,458000,433500,642600,409600,363100,430100,503900,500400,557400,565500,526700,628900,547700,520400,731200,494400,416800,558700,537100,556200,686700,616600,582600,725800,577700,552100,806700,554200,455000,532600,693000,619400,727100,684700)
y<-ts(x,frequency=12, start=c(1976,1))
#Transforming the data to log or sqrt and plotting it
log.y<-log(y)
plot(log.y)
sqrt.y<-sqrt(y)
plot(sqrt.y)
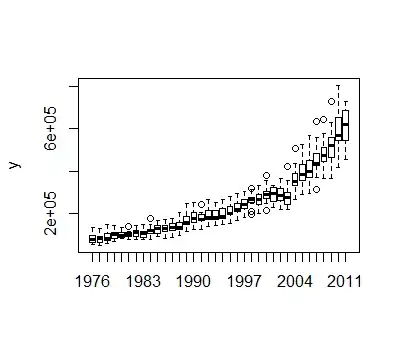
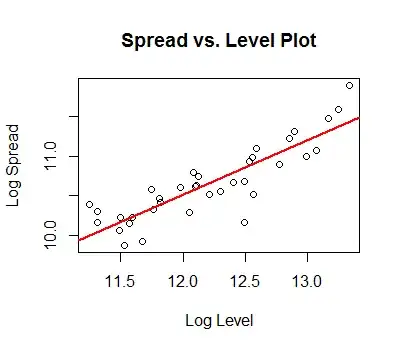
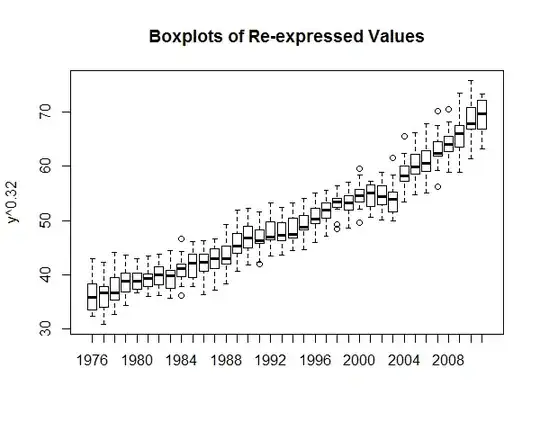
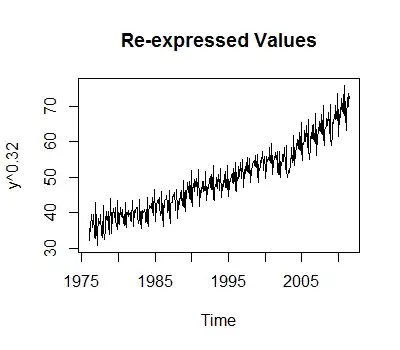
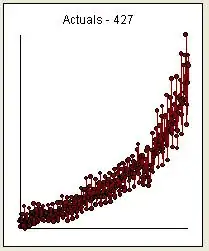 suggests a series that has structural change. The Chow Test yielded a signifciant break point
suggests a series that has structural change. The Chow Test yielded a signifciant break point 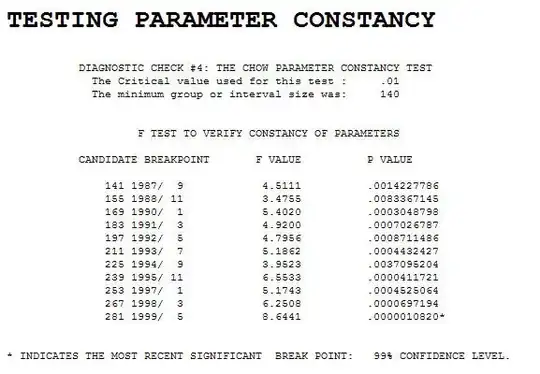 .
. 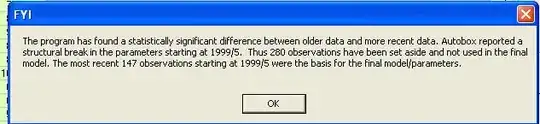 . Analysis of the modt recent 147 values starting at 1999/5 yielded
. Analysis of the modt recent 147 values starting at 1999/5 yielded 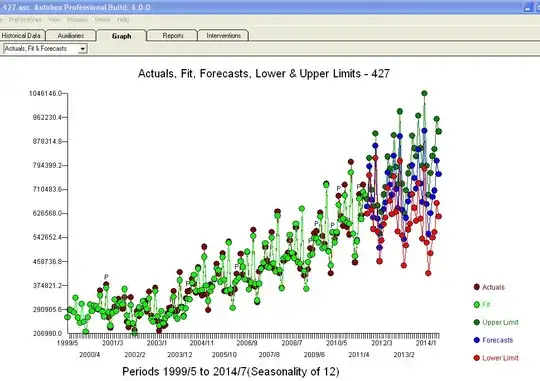 with a Residual Plot
with a Residual Plot 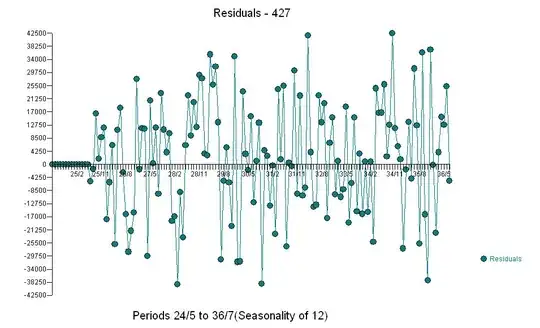 with the following ACF
with the following ACF  . The forecast plot is
. The forecast plot is 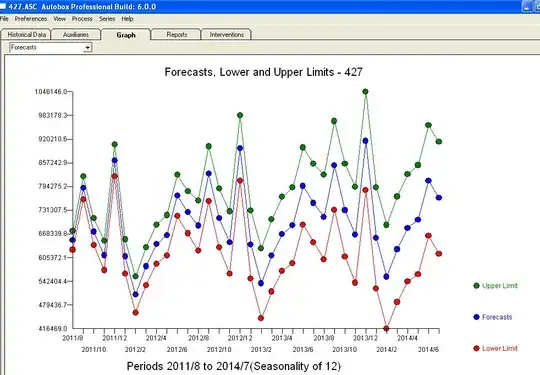 . The final model is
. The final model is 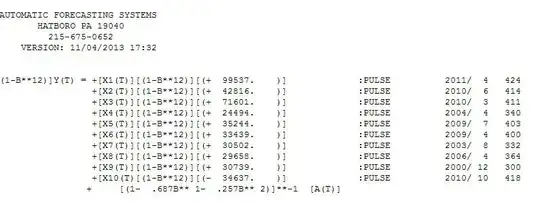 with all parameters statistically significant and no unwarranted power transformations which often unfortunately lead to wildly explosive and unrealistic forecasts. Power transforms are justified whrn it is proven via a Box-Cox test that the variablility of the ERRORS is related to the expected value as detailed here. N.B. that the variability of the original series is not used but the variability of model errors.
with all parameters statistically significant and no unwarranted power transformations which often unfortunately lead to wildly explosive and unrealistic forecasts. Power transforms are justified whrn it is proven via a Box-Cox test that the variablility of the ERRORS is related to the expected value as detailed here. N.B. that the variability of the original series is not used but the variability of model errors.