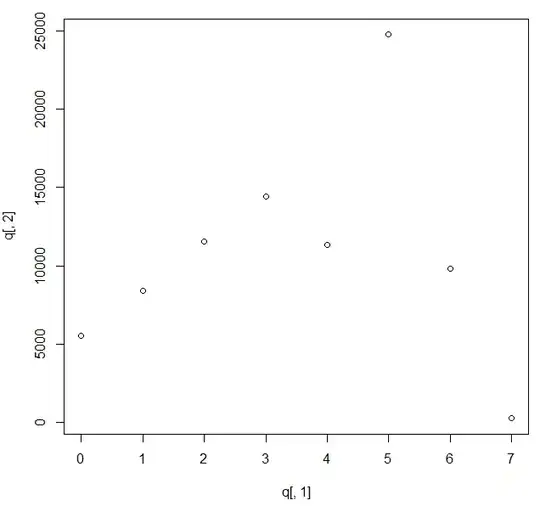
I have a count dataset that contains many zeros and a discrete variable that contains many zeros as well. I would like to see graphically which kind of correlation exists between these two variables.
When I try in R to plot these two variables (plot(X, Y))) I get something that I'm not able to interpret.
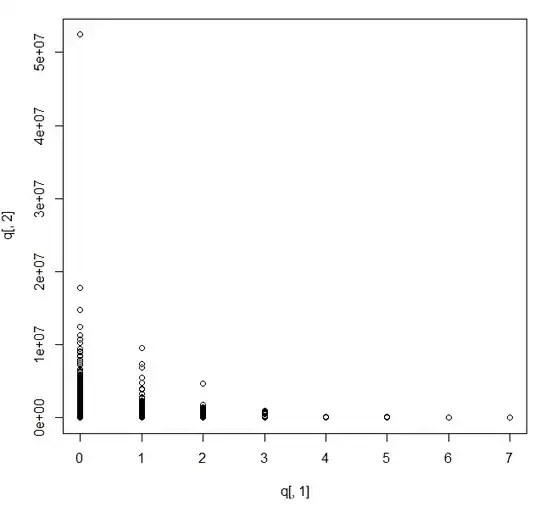
Is there any data transformation that could help me to graphically identify the relation between these two variables?
I add also the histograms for the two variables, mean and sd
In the figure below, the mean of q[,2] given q[,1]