PCA computes eigenvectors of the covariance matrix ("principal axes") and sorts them by their eigenvalues (amount of explained variance). The centered data can then be projected onto these principal axes to yield principal components ("scores"). For the purposes of dimensionality reduction, one can keep only a subset of principal components and discard the rest. (See here for a layman's introduction to PCA.)
Let $\mathbf X_\text{raw}$ be the $n\times p$ data matrix with $n$ rows (data points) and $p$ columns (variables, or features). After subtracting the mean vector $\boldsymbol \mu$ from each row, we get the centered data matrix $\mathbf X$. Let $\mathbf V$ be the $p\times k$ matrix of some $k$ eigenvectors that we want to use; these would most often be the $k$ eigenvectors with the largest eigenvalues. Then the $n\times k$ matrix of PCA projections ("scores") will be simply given by $\mathbf Z=\mathbf {XV}$.
This is illustrated on the figure below: the first subplot shows some centered data (the same data that I use in my animations in the linked thread) and its projections on the first principal axis. The second subplot shows only the values of this projection; the dimensionality has been reduced from two to one:
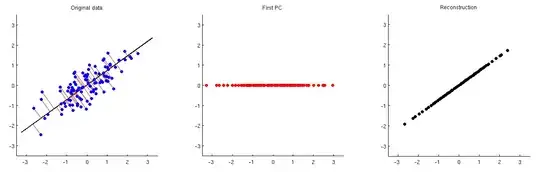
In order to be able to reconstruct the original two variables from this one principal component, we can map it back to $p$ dimensions with $\mathbf V^\top$. Indeed, the values of each PC should be placed on the same vector as was used for projection; compare subplots 1 and 3. The result is then given by $\hat{\mathbf X} = \mathbf{ZV}^\top = \mathbf{XVV}^\top$. I am displaying it on the third subplot above. To get the final reconstruction $\hat{\mathbf X}_\text{raw}$, we need to add the mean vector $\boldsymbol \mu$ to that:
$$\boxed{\text{PCA reconstruction} = \text{PC scores} \cdot \text{Eigenvectors}^\top + \text{Mean}}$$
Note that one can go directly from the first subplot to the third one by multiplying $\mathbf X$ with the $\mathbf {VV}^\top$ matrix; it is called a projection matrix. If all $p$ eigenvectors are used, then $\mathbf {VV}^\top$ is the identity matrix (no dimensionality reduction is performed, hence "reconstruction" is perfect). If only a subset of eigenvectors is used, it is not identity.
This works for an arbitrary point $\mathbf z$ in the PC space; it can be mapped to the original space via $\hat{\mathbf x} = \mathbf{zV}^\top$.
Discarding (removing) leading PCs
Sometimes one wants to discard (to remove) one or few of the leading PCs and to keep the rest, instead of keeping the leading PCs and discarding the rest (as above). In this case all the formulas stay exactly the same, but $\mathbf V$ should consist of all principal axes except for the ones one wants to discard. In other words, $\mathbf V$ should always include all PCs that one wants to keep.
Caveat about PCA on correlation
When PCA is done on correlation matrix (and not on covariance matrix), the raw data $\mathbf X_\mathrm{raw}$ is not only centered by subtracting $\boldsymbol \mu$ but also scaled by dividing each column by its standard deviation $\sigma_i$. In this case, to reconstruct the original data, one needs to back-scale the columns of $\hat{\mathbf X}$ with $\sigma_i$ and only then to add back the mean vector $\boldsymbol \mu$.
Image processing example
This topic often comes up in the context of image processing. Consider Lenna -- one of the standard images in image processing literature (follow the links to find where it comes from). Below on the left, I display the grayscale variant of this $512\times 512$ image (file available here).

We can treat this grayscale image as a $512\times 512$ data matrix $\mathbf X_\text{raw}$. I perform PCA on it and compute $\hat {\mathbf X}_\text{raw}$ using the first 50 principal components. The result is displayed on the right.
Reverting SVD
PCA is very closely related to singular value decomposition (SVD), see
Relationship between SVD and PCA. How to use SVD to perform PCA? for more details. If a $n\times p$ matrix $\mathbf X$ is SVD-ed as $\mathbf X = \mathbf {USV}^\top$ and one selects a $k$-dimensional vector $\mathbf z$ that represents the point in the "reduced" $U$-space of $k$ dimensions, then to map it back to $p$ dimensions one needs to multiply it with $\mathbf S^\phantom\top_{1:k,1:k}\mathbf V^\top_{:,1:k}$.
Examples in R, Matlab, Python, and Stata
I will conduct PCA on the Fisher Iris data and then reconstruct it using the first two principal components. I am doing PCA on the covariance matrix, not on the correlation matrix, i.e. I am not scaling the variables here. But I still have to add the mean back. Some packages, like Stata, take care of that through the standard syntax. Thanks to @StasK and @Kodiologist for their help with the code.
We will check the reconstruction of the first datapoint, which is:
5.1 3.5 1.4 0.2
Matlab
load fisheriris
X = meas;
mu = mean(X);
[eigenvectors, scores] = pca(X);
nComp = 2;
Xhat = scores(:,1:nComp) * eigenvectors(:,1:nComp)';
Xhat = bsxfun(@plus, Xhat, mu);
Xhat(1,:)
Output:
5.083 3.5174 1.4032 0.21353
R
X = iris[,1:4]
mu = colMeans(X)
Xpca = prcomp(X)
nComp = 2
Xhat = Xpca$x[,1:nComp] %*% t(Xpca$rotation[,1:nComp])
Xhat = scale(Xhat, center = -mu, scale = FALSE)
Xhat[1,]
Output:
Sepal.Length Sepal.Width Petal.Length Petal.Width
5.0830390 3.5174139 1.4032137 0.2135317
For worked out R example of PCA reconstruction of images see also this answer.
Python
import numpy as np
import sklearn.datasets, sklearn.decomposition
X = sklearn.datasets.load_iris().data
mu = np.mean(X, axis=0)
pca = sklearn.decomposition.PCA()
pca.fit(X)
nComp = 2
Xhat = np.dot(pca.transform(X)[:,:nComp], pca.components_[:nComp,:])
Xhat += mu
print(Xhat[0,])
Output:
[ 5.08718247 3.51315614 1.4020428 0.21105556]
Note that this differs slightly from the results in other languages. That is because Python's version of the Iris dataset contains mistakes.
Stata
webuse iris, clear
pca sep* pet*, components(2) covariance
predict _seplen _sepwid _petlen _petwid, fit
list in 1
iris seplen sepwid petlen petwid _seplen _sepwid _petlen _petwid
setosa 5.1 3.5 1.4 0.2 5.083039 3.517414 1.403214 .2135317

