I would like to remove the first principal component from a data set, but keep that data set in its original coordinates. I have taken a stab at this by taking PCA, zeroing the first PC, and then rotating back using the inverse of the eigvenvector matrix. Is that the most efficient way to do this?
create a sample data set:
set.seed(1234)
xx <- rnorm(500)
yy <- 0.5 * xx + rnorm(500, sd = 0.3)
vec <- cbind(xx, yy)
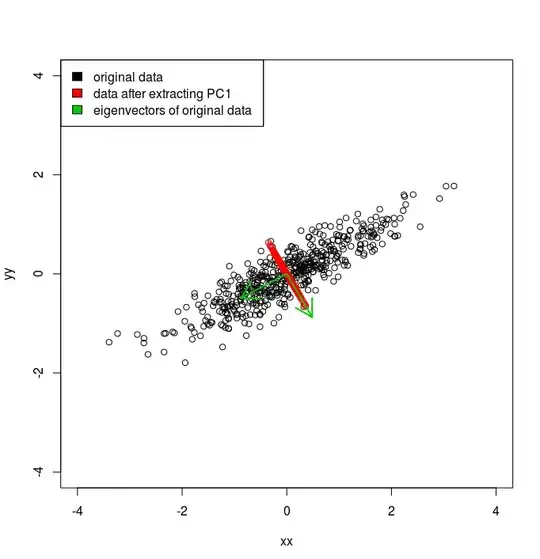
plot(vec, xlim = c(-4, 4), ylim = c(-4, 4))
Take principal components and zero out the first PC:
vv <- eigen(cov(vec))$vectors
newvec <- vec %*% vv
newvec[, 1] <- 0
Now rotate the new data set back to its original coordinates using the inverse of the PCA rotation matrix:
rvec <- newvec %*% t(vv) # transpose of orthogonal matrix = inverse
# plot new points in red and plot eigenvectors in green
points(rvec, col = "red")
arrows(0, 0, vv[1,1], vv[2, 1], col = "green3", lwd = 2)
arrows(0, 0, vv[1,2], vv[2, 2], col = "green3", lwd = 2)
legend("topleft", legend = c("original data", "data after extracting PC1", "eigenvectors of original data"), fill = c("black", "red", "green3"))
As you can see it seems to agree with the eigenvector orientations in green. But is this the correct and/or best way? Can I avoid the intermediate matrix multiplications for example?