25

I am an enthusiast of programming and machine learning. Only a few months back I started learning about machine learning programming. Like many who don't have a quantitative science background I also started learning about ML by tinkering with the algorithms and datasets in the widely used ML package(caret R).

A while back I read a blog in which the author talks about usage of linear regression in ML. If I am remembering correct he talked about how all machine learning in the end uses some kind of "linear regression"(not sure whether he used this exact term) even for linear or non-linear problems. That time I didn't understood what he meant by that.

My understanding of using machine learning for non-linear data is to use a non linear algorithm to separate the data.

This was my thinking

Let's say to classify linear data we used linear equation $y=mx+c$ and for non linear data we use non-linear equation say $y=sin(x)$

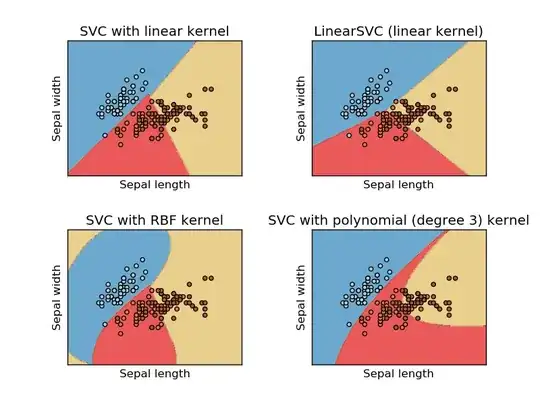
enter image description here

This image is taken from sikit learn website of support vector machine. In SVM we used different kernels for ML purpose. So my initial thinking was linear kernel separates the data using a linear function and RBF kernel uses a non-linear function to separate the data.

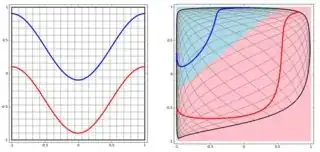
But then I saw this blog where the author talks about Neural networks.

To classify the non linear problem in left subplot, the neural network transforms the data in such a way that in the end we can use simple linear separation to the transformed data in the right sub-plot

enter image description here

My question is whether all machine learning algorithms in the end uses a linear separation to classifiction(linear /non-linear dataset)?

whuber
  • 281,159
  • 54
  • 637
  • 1,101
Eka
  • 1,921
  • 2
  • 22
  • 28
  • 1
    Related: http://stats.stackexchange.com/questions/164048/can-random-forest-be-used-for-feature-selection-in-multiple-linear-regression/164068#164068 – Sycorax Jun 01 '16 at 15:24
  • 3
    Your non-linear model $\sin(x)$ is also a linear. introduce a new variable $s=\sin(x)$, then your problem becomes $y=\theta_0+\theta_1 s$ - a linear one. In this sense a lot of ML algos are linear indeed. – Aksakal Jun 22 '16 at 14:03
  • I like mbq's answer on this thread as well, [Help me understand support vector machines](http://stats.stackexchange.com/a/3954/1036). – Andy W Jun 24 '16 at 14:48

2 Answers2

26

The answer is No. user20160 has a perfect answer, I will add 3 examples with visualization to illustrate the idea. Note, these plots may not be helpful for you to see if the "final decision" is in linear form but give you some sense about tree, boosting and KNN.

We will start with decision trees. With many splits, it is a non-linear decision boundary. And we cannot think all the previous splits are "feature transformations" and there are a final decision line at the end.

Another example is the boosting model, which aggregates many "weak classifiers" and the final decision boundary is not linear. You can think about it is a complicated code/algorithm to make the final prediction.

Finally, think about K Nearest Neighbors (KNN). It is also not a linear decision function at the end layer. in addition, there are no "feature transformations" in KNN.

Here are three visualizations in 2D space (Tree, Boosting and KNN from top to bottom). The ground truth is 2 spirals represent two classes, and the left subplot is the predictions from the model and the right subplot is the decision boundaries from the model.

Tree decision boundary

Boosting decision boundary

KNN decision boundary

EDIT: @ssdecontrol's answer in this post gives another perspective.

It depends on how we define the "transformation".

Any function that partitions the data into two pieces can be transformed into a linear model of this form, with an intercept and a single input (an indicator of which "side" of the partition the data point is on). It is important to take note of the difference between a decision function and a decision boundary.

Community
  • 1
Haitao Du
  • 32,885
  • 17
  • 118
  • 213
  • I don't want to critic, but the boosting seems a bit rough, no? Is it not possible to get a smoother result with different parameters? Sorry to be pernickety, because I find the all explanation very good. – YCR Jun 01 '16 at 15:56
  • @YCR I think that is the point of boosting where you have a rough decision boundary. The roughness is caused by aggregating many weak classifiers (in this example,they are trees). But I agree with you that the second example is not a good model, and it is overfitting :) – Haitao Du Jun 01 '16 at 16:53
  • 1
    (+1) Great visualization (I also use `spirals` a lot in my experimentations). A suggestion: plot the decision boundaries as `image`, and perhaps add probabiliity levels (if you are using probabilistic outputs) with `contour`. – Firebug Jun 24 '16 at 14:22
  • @Firebug great suggestion! these plot are generated in a grid and only can tell you the final label. Contour is much better. – Haitao Du Jun 24 '16 at 14:27
  • Look at my answer here: http://stats.stackexchange.com/a/218578/60613 – Firebug Jun 24 '16 at 14:45
  • The frequent occurrence of tiny edits suggests you are no longer improving the post, but only attempting to draw attention to it. Your attention to detail and dedication to getting it right are admirable, but there is a cost: the entire thread keeps popping up in the queue. People will tire of reviewing it. Please limit edits to important changes that are clear improvements--such as fixing errors or clarifying the post. A better way to bring attention to a well-crafted answer is to post comments (or substantial answers) in related threads and provide links back here. – whuber Jun 28 '16 at 15:43
  • @hxd1011 Can you tell me why is the linear seperability required. For instance the left image https://i.stack.imgur.com/wOCJM.png can very well be classified using a circle, why then take all pain & transform it to right image – vinita Jul 31 '17 at 15:03
  • @vinita i think it is a good and separate question, why not ask it and I will try to write an answer. – Haitao Du Jul 31 '17 at 15:09
  • @hxd1011 Here you go https://stats.stackexchange.com/questions/295421/why-is-it-desirable-to-have-linear-separability-in-svm – vinita Aug 01 '17 at 11:00
21

Some algorithms use a hyperplane (i.e. linear function) to separate the data. A prominent example is logistic regression. Others use a hyperplane to separate the data after a nonlinear transformation (e.g. neural networks and support vector machines with nonlinear kernels). In this case, the decision boundary is nonlinear in the original data space, but linear in the feature space into which the data are mapped. In the case of SVMs, the kernel formulation defines this mapping implicitly. Other algorithms use multiple splitting hyperplanes in local regions of data space (e.g. decision trees). In this case, the decision boundary is piecewise linear (but nonlinear overall).

However, other algorithms have nonlinear decision boundaries, and are not formulated in terms of hyperplanes. A prominent example is k nearest neighbors classification. Ensemble classifiers (e.g. produced by boosting or bagging other classifiers) are generally nonlinear.

user20160
  • 29,014
  • 3
  • 60
  • 99
  • 1
    @CagdasOzgenc Let's consider the case of binary classification and a network w/ sigmoidal output, as you're suggesting. This is equivalent to logistic regression on the activations of the previous layer (using softmax outputs would be equivalent to multinomial logistic regression). So, the decision boundary is a hyperplane in feature space. The picture in the original question shows a nice example of this. – user20160 Jun 22 '16 at 21:06
  • Is f the output neuron's activation function and x the output of the previous layer? Not sure I understand what you're asking. – user20160 Jun 23 '16 at 11:25
  • Say we determine the class label by comparing the output to some threshold. If $f$ is non-invertible, it seems like that could induce multiple, parallel hyperplanes (all orthogonal to $Ax$). That would certainly be a unique output neuron. – user20160 Jun 23 '16 at 11:44
  • The decision boundaries should still be linear no matter what f is, as long as it operates on Ax. But it's true, we could imagine functions that operate on x more generally, which could give nonlinear boundaries. Fun to think about. – user20160 Jun 23 '16 at 12:18
  • How about decision trees? – Harold Ship Jun 27 '16 at 18:35
  • Mentioned these in the first paragraph. They're an interesting case. – user20160 Jun 27 '16 at 21:52