Why sigmoid function in logistic regresion can make good estimations on non-linear data?

Question

If I understood correctly, then in the logistic regression we select the parameters of the sigmoid function so that it maximally approximates the input data. I can understand why logistic regression works fine when data distributed like in this photo. But why it still works fine with data like in this photo?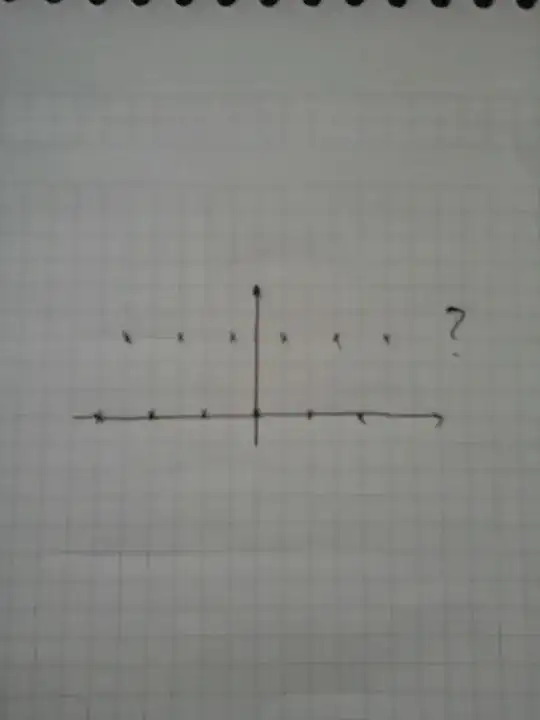 How to approximate it correctly? I'm sorry for bad quality of photoes.

Answer 1

In the last example provided, given information only on $x$ and $y$, logistic regression will be unable to find a good solution. Logistic regression is a linear method in the parameters. Before continuing let's take a step back and see why we use the sigmoid to begin with.

Say we tried to categorise our $[X,y]$ where $y$ is either $0$ or $1$ data with linear regression. The problem here would be obviously that the estimates $ X\hat{\beta}$ are not constrained, ie. $-\infty \leq X\hat{\beta} \leq +\infty$. OK, not so good, we need these guys to be always non-negative. Let's exponentiate them! Grant! So we get $0 \leq \exp(X\hat{\beta}) \leq +\infty$. Progress! But still not good enough, we get values above $1$. No problem! Let's divide them by the maximal value they can get! So we get $0 \leq \frac{\exp(X\hat{\beta})}{ 1 + \exp(\hat{X\beta})} \leq 1$. OK, double exponentiation sees cumbersome can we simplify it? Sure thing: $0 \leq \frac{1}{ 1 + \exp(-\hat{X\beta})} \leq 1$. And we just got back the standard sigmoid function.

As we see, the sigmoid function is just a non-linear but still monotonic projection of our original linear estimates. So if our original data $x$ and $y$ are like the one shown in the last photo of the post, there is no way we get any reasonable hyperplane differentiating between instances of $y=1$ and $y=0$. (Yes, we might recognise some periodicity, etc. etc. but these steps will entail augmenting our design matrix $X$ with these transformations)

There is an excellent question on CV on :"Do all machine learning algorithms separate data linearly?" which I think will complement your understanding of this issues further.