21

Decision stump is a decision tree with only one split. It can also be written as a piecewise function.

For example, assume $x$ is a vector, and $x_1$ is the first component of $x$, in regression setting, some decision stump can be

$f(x)= \begin{cases} 3& x_1\leq 2 \\ 5 & x_1 > 2 \\ \end{cases} $

But is it a linear model? where can be written as $f(x)=\beta^T x$? This Question may sound strange, because as mentioned in the answers and comments, if we plot the piecewise function it is not a line. Please see next section for why I am asking this question.

EDIT:

  • The reason I ask this question is logistic regression is a (generalized) linear model and the decision boundary is a line, also for decision stump. Note, we also have this question: Why is logistic regression a linear model? . On the other hand, it seems not true that decision stump is a linear model.

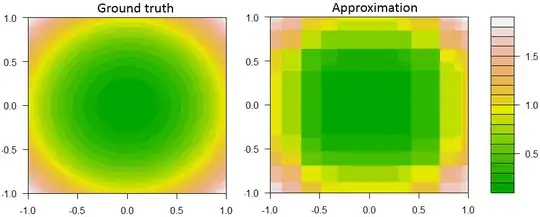
enter image description here

Here is one example of decision stump boosting on regression with 2 features and 1 continuous response.

enter image description here

Community
  • 1
Haitao Du
  • 32,885
  • 17
  • 118
  • 213
  • Why would you consider it to be linear..? – Tim Aug 23 '16 at 14:49
  • 5
    @hxd1011 important to distinguish between the decision boundary and the decision function here – shadowtalker Aug 23 '16 at 14:56
  • I could call it a 1000th order polynomial with all orders from 1 to 1000 equal zero. I could call it a zero-order (aka constant) model and it would more succinctly communicate the key features. A classic tree is piecewise constant. The trivial tree, a stump, is a single split in the space where the model on one side is constant and the the other is a different constant. It isn't globally constant, but it isn't poly1 either. The "cubist" library in R fits with actual linear (poly1) models instead of constant models. You might try that. – EngrStudent Aug 23 '16 at 15:01
  • 1
    If you draw a line in the plane (say y = 0), and take *any* function $f(x)$, then $g(x, y) = f(x)$ will have contour lines which are actual lines (parallel to the $y$ axis), but it will *not* be a linear function. – Matthew Drury Aug 23 '16 at 15:45
  • If we pretend like we know that the split happens when x1 is equal to 2 then we can write it as a linear model. Decision trees/stumps don't do this though - that part is estimated. So if we are considering the split value to be estimated then it isn't a linear model. – Dason Aug 23 '16 at 17:29
  • Generalized Linear Model =/= Linear Model – Hao Ye Aug 23 '16 at 22:43
  • 1
    This is a strange question. Can you plot the function from your example (which is equal to 3 for x<2 and 5 for x>2)? Look at it -- is it a straight line? If it is not a straight line, then it is not a linear function. – amoeba Aug 23 '16 at 22:43
  • 1
    @amoeba, i agree with you, the function plot is a not linear. I think my question is confusing also because it is not really clear what is "linear model" – Haitao Du Aug 24 '16 at 05:13

3 Answers3

22

No, unless you transform the data.

It is a linear model if you transform $x$ using indicator function: $$ x' = \mathbb I \left(\{x>2\}\right) = \begin{cases}\begin{align} 0 \quad &x\leq 2\\ 1 \quad &x>2 \end{align}\end{cases} $$

Then $f(x) = 2x' + 3 = \left(\matrix{3 \\2}\right)^T \left(\matrix{1 \\x'}\right)$

Edit: this was mentioned in the comments but I want to emphasize it here as well. Any function that partitions the data into two pieces can be transformed into a linear model of this form, with an intercept and a single input (an indicator of which "side" of the partition the data point is on). It is important to take note of the difference between a decision function and a decision boundary.

shadowtalker
  • 11,395
  • 3
  • 49
  • 109
8

Answers to your questions:

  1. A decision stump is not a linear model.
  2. The decision boundary can be a line, even if the model is not linear. Logistic regression is an example.
  3. The boosted model does not have to be the same kind of model as the base learner. If you think about it, your example of boosting, plus the question you linked to, proves that the decision stump is not a linear model.
Flounderer
  • 9,575
  • 1
  • 32
  • 43
3

This answer is more verbose than is needed to just answer the question. I hope to provoke some comments from real experts.

I once was in a court room and the judge asked (for good reason in context) , if we call a dog's tail a leg, does that mean a dog has 5 legs ? So what is a linear model ?

In the context of statistics I've been told by an expert that a linear model means a statistical model constructed from a set of functions $ f_1, f_2, \ldots, f_n$ of the form $ y = \sum a_i f_i $ with the important constraint that the error terms are independent and normally distributed. With that definition, one can't say if your model is linear because you have given no information about the error term. If one drops the error term constraint, then it is tautologically linear in the function you give or in the function ssdecontrol gives. However naively, in the context of this question, that may be unsatisfactory. Any function can be considered as the basis of a linear in that sense. That is because any space of functions can be turned into a vector space of functions.

If you are asking on the nose, that is mathematically, if your function linear, then the answer is no. A linear function is one whose graph is a straight line, while clearly your function doesn't have that property. In answer to the question you pose at the end, that is can one find $\beta$ so that $ f(x) = \beta^{T} x $ , then no.

Any function of the class you give would satisfy $f(x+y) = f(x) + f(y) $ for any (real) numbers $x$ and $y$. Notice that your function satisfies $ f(1.5) = 3$ and $f(3) = 5$, so $ f(3) \neq f(1.5) + f(1.5)$ as would be required if your function was of the form $f(x) = \beta^T x$. Notice the class you propose for linear functions is a sub-class of what are usually called linear functions.

Haitao Du
  • 32,885
  • 17
  • 118
  • 213
meh
  • 1,902
  • 13
  • 18
  • 4
    Linearity has nothing to do with error terms. It has to do with the fact that it consists of a _linear combination of the parameters_. This represents a straight line in 2D space (but more generally represents a plane). – shadowtalker Aug 23 '16 at 16:12
  • @ssdecontrol - I can only tell you that a probability Ph.D. (and a student of Kolmogorov at that) insisted to me that the term 'linear model', when used in statistics, included a statement about the error term. I'm actually very interested in how common this view might be. Linear has many meanings. For example, if one has an equation in N space $f(x) = 0 $, then we could say it is linear if the zero set is a hyperplane. Of course that would mean we could write $ f(x) = a_0 + \sum_{i=1}^{i=N} a_ix_i $ . However the function would be linear $\iff a_0 = 0$ i.e. $f(x+y) = f(x) + f(y) $. – meh Aug 24 '16 at 13:28
  • if that's what he insists, then that's his opinion and not some kind of hard fact. As far as I'm aware, there is no rigorous accepted definition for a "linear model", nor is there a need for one in my mind. For me, the fact that there is an error term involved just turns the model from a "linear model" to a "statistical linear model". I don't see anything inherently linear about her terms, nor do I see anything inherently statistical about linear models. – shadowtalker Aug 24 '16 at 15:44
  • IMO insisting on the presence of an error term just discounts what, say, and engineering or physicist might deem a "linear model" of a deterministic physical process. – shadowtalker Aug 24 '16 at 15:44