Given a data scatterplot I can plot the data's principal components on it, as axes tiled with points which are principal components scores. You can see an example plot with the cloud (consisting of 2 clusters) and its first principle component. It is drawn easily: raw component scores are computed as data-matrix x eigenvector(s); coordinate of each score point on the original axis (V1 or V2) is score x cos-between-the-axis-and-the-component (which is the element of the eigenvector).
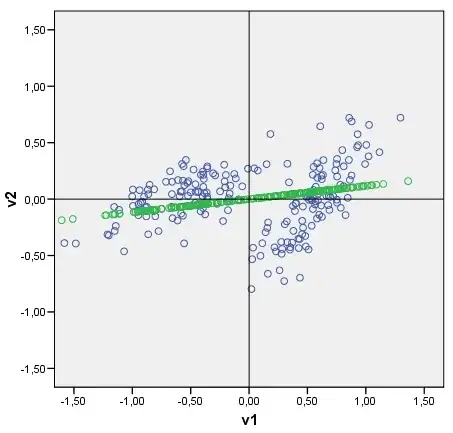
My question: Is it possible somehow to draw a discriminant in a similar fashion? Look at my pic please. I'd like to plot now the discriminant between two clusters, as a line tiled with discriminant scores (after discriminant analysis) as points. If yes, what could be the algo?