Change point analysis using R's nls()

Question

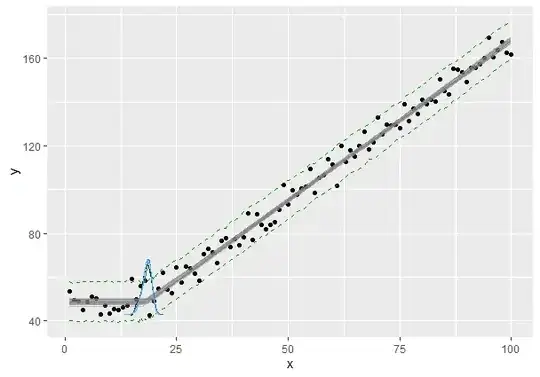
I'm trying to implement a "change point" analysis, or a multiphase regression using nls() in R.

Here's some fake data I've made. The formula I want to use to fit the data is:

$y = \beta_0 + \beta_1x + \beta_2\max(0,x-\delta)$

What this is supposed to do is fit the data up to a certain point with a certain intercept and slope ($\beta_0$ and $\beta_1$), then, after a certain x value ($\delta$), augment the slope by $\beta_2$. That's what the whole max thing is about. Before the $\delta$ point, it'll equal 0, and $\beta_2$ will be zeroed out.

So, here's my function to do this:

changePoint <- function(x, b0, slope1, slope2, delta){ 
   b0 + (x*slope1) + (max(0, x-delta) * slope2)
}

And I try to fit the model this way

nls(y ~ changePoint(x, b0, slope1, slope2, delta), 
    data = data, 
    start = c(b0 = 50, slope1 = 0, slope2 = 2, delta = 48))

I chose those starting parameters, because I know those are the starting parameters, because I made the data up.

However, I get this error:

Error in nlsModel(formula, mf, start, wts) : 
  singular gradient matrix at initial parameter estimates

Have I just made unfortunate data? I tried fitting this on real data first, and was getting the same error, and I just figured that my initial starting parameters weren't good enough.

score 13 · Accepted Answer · edited May 12 '15 at 07:52

(At first I thought it could be a problem resulting from the fact that max is not vectorized, but that's not true. It does make it a pain to work with changePoint, wherefore the following modification:

changePoint <- function(x, b0, slope1, slope2, delta) { 
   b0 + (x*slope1) + (sapply(x-delta, function (t) max(0, t)) * slope2)
}

This R-help mailing list post describes one way in which this error may result: the rhs of the formula is overparameterized, such that changing two parameters in tandem gives the same fit to the data. I can't see how that is true of your model, but maybe it is.

In any case, you can write your own objective function and minimize it. The following function gives the squared error for data points (x,y) and a certain value of the parameters (the weird argument structure of the function is to account for how optim works):

sqerror <- function (par, x, y) {
  sum((y - changePoint(x, par[1], par[2], par[3], par[4]))^2)
}

Then we say:

optim(par = c(50, 0, 2, 48), fn = sqerror, x = x, y = data)

And see:

$par
[1] 54.53436800 -0.09283594  2.07356459 48.00000006

Note that for my fake data (x <- 40:60; data <- changePoint(x, 50, 0, 2, 48) + rnorm(21, 0, 0.5)) there are lots of local maxima depending on the initial parameter values you give. I suppose if you wanted to take this seriously you'd call the optimizer many times with random initial parameters and examine the distribution of results.

[This post](http://www.biostat.wustl.edu/archives/html/s-news/1999-07/msg00212.html) by Bill Venables explains well the issues involved in this kind of analysis. — Aaron, Feb 23 '11 at 07:07
Instead of that (cumbersome) **sapply** call in your first code snippet, you can always just use **pmax**. — cardinal, Apr 14 '11 at 19:00

score 1 · Answer 2 · answered Jan 10 '20 at 11:13

Just wanted to add that you can do this with many other packages. If you want to get an estimate of uncertainty around the change point (something nls cannot do), try the mcp package.

# Simulate the data
df = data.frame(x = 1:100)
df$y = c(rnorm(20, 50, 5), rnorm(80, 50 + 1.5*(df$x[21:100] - 20), 5))

# Fit the model
model = list(
  y ~ 1,  # Intercept
  ~ 0 + x  # Joined slope
)
library(mcp)
fit = mcp(model, df)

Let's plot it with a prediction interval (green line). The blue density is the posterior distribution for the change point location:

# Plot it
plot(fit, q_predict = T)

You can inspect individual parameters in more detail using plot_pars(fit) and summary(fit).

Change point analysis using R's nls()

2 Answers2

Linked

Related