Note: In this simplified linear model, the OLS estimator $\hat\beta(y)$ is a sufficient statistic, meaning that the posterior on the parameters is the same given $y$ and given $\hat\beta(y)$.
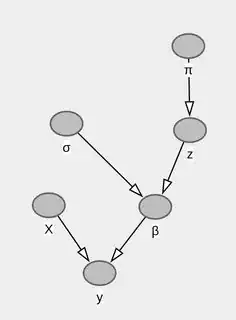
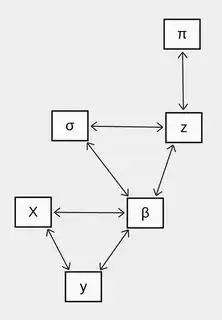
Left graph is a (directed acyclic) graph representing the dependence structure in the model. Right graph is the so-called moral graph associated with it (where parents are linked). It is most useful to find conditional dependencies for building a Gibbs sampler, as a node is independent of everything else given its neighbours, i.e. parents and children. For instance, $\beta$ only depends on $y$, $z$, $X$, and $\sigma=(\sigma_1,\sigma_2)$, but not on $\pi$.
$$
\beta| z, \sigma_1, \sigma_2, y\sim f(\beta| z, \sigma_1, \sigma_2,y)\propto f(\beta| z, \sigma_1, \sigma_2)\times f(y|,\beta,X)
$$
Similarly, $z$ only depends on $\pi$, $\sigma$, and $\beta$, and not on $y$. And at last $\pi$ solely depends on $z$,$$f(\pi|z,\ldots,y)=f(\pi|z)$$
When considering the full conditional of one component of $\beta$, like $\beta_1$, the density satisfies
$$f(\beta_1|\beta_{-1},z, \sigma_1, \sigma_2, y)\sim f(\beta_1| z, \sigma_1, \sigma_2,y)\propto f(\beta| z, \sigma_1, \sigma_2,y)$$
which only depends on $z_1$ (and not $z_2,z_3,z_4$):
$$f(\beta_1|\beta_{-1},z, \sigma_1, \sigma_2, y)\sim f(\beta_1| z, \sigma_1, \sigma_2,y)\propto f(\beta_1| z_1, \sigma_1, \sigma_2)\times f(y|X,\beta)$$
Although this should be considered as a separate question, here are the details when running a full conditional Gibbs sampler on $\beta$:
At step 0, start with an arbitrary vector $\beta^{(0)}$ (for instance, the OLS $\hat\beta(y)$, and $\pi^{(0)}$, and generate $z^{(0)}$ from its full conditional distribution.
At step t, given the current state $\beta^{(t)},\sigma^{(t)},z^{(t)},\pi^{(t)}$ of the parameter, do
- update $\beta_1^{(t)}$ into $\beta_1^{(t+1)}$ by simulating from
$$f(\beta_1|\beta_2^{(t)},\beta_3^{(t)},\beta_4^{(t)}, z^{(t)}, \sigma^{(t)},y)\propto f(\beta_1|z_1^{(t)}, \sigma^{(t)})\times
f(y|\beta_1,\beta_2^{(t)},\beta_3^{(t)},\beta_4^{(t)})$$
- update $\beta_2^{(t)}$ into $\beta_2^{(t+1)}$ by simulating from
$$f(\beta_2|\beta_1^{(t+1)},\beta_3^{(t)},\beta_4^{(t)}, z^{(t)}, \sigma^{(t)},y)\propto f(\beta_2|z_2^{(t)}, \sigma^{(t)})\times
f(y|\beta_1^{(t+1)},\beta_2,\beta_3^{(t)},\beta_4^{(t)})$$
- update $\beta_3^{(t)}$ into $\beta_3^{(t+1)}$ by simulating from
$$f(\beta_3|\beta_1^{(t+1)},\beta_2^{(t+1)},\beta_4^{(t)}, z^{(t)}, \sigma^{(t)},y)\propto f(\beta_3|z_3^{(t)}, \sigma^{(t)})\times
f(y|\beta_1^{(t+1)},\beta_2^{(t+1)},\beta_3,\beta_4^{(t)})$$
- update $\beta_4^{(t)}$ into $\beta_4^{(t+1)}$ by simulating from
$$f(\beta_4|\beta_1^{(t+1)},\beta_2^{(t+1)},\beta_3^{(t+1)}, z^{(t)}, \sigma^{(t)},y)\propto f(\beta_4|z_4^{(t)}, \sigma^{(t)})\times
f(y|\beta_1^{(t+1)},\beta_2^{(t+1)},\beta_3^{(t+1)},\beta_4)$$

