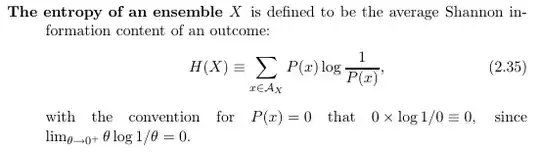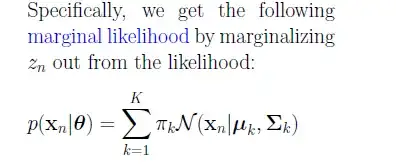I am studying gaussian mixture models. The first step defines the following equation.
They then proceed to marginalize $z_n$ out
My question is, how did they arrive at that equation ? Where did the product over $K$ go to ? Marginalizing over $z_n$ means to sum over $z_n$. But there was a multiplication over $n$ in the original equation. What happened to it ?
The first equation, $p(\textbf{X, z} \mid \bf{\theta})$ refers to the joint likelihood function of all observed data, $\textbf{X} = x_1, x_2, \ldots, x_N$ and the latent variables, $\textbf{z} = z_1, z_2, \ldots, z_N$, given the model parameters, $\bf{\theta} \equiv \{\bf{\mu, \Sigma, \pi}\}$ hence the first equation has a product over $N$ and $K$.
The second equation refers to the likelihood of a single observation, $p(x_n \mid \bf{\theta})$. It comes from the following intuition,
Given the latent variable assignment, $z_n = k$, the given observation $x_n$ is drawn from the $k^{th}$ Gaussian component of the mixture model.
$$ p(x_n \mid z_n = k, \theta) = \mathcal{N}(\mu_k, \Sigma_k) $$
Now, for a given observation, if you marginalize $z_n$, you get
$$ \begin{align} p(x_n \mid \theta) &= \sum_{k=1}^{K} p(z_n = k) \times p(x_n \mid z_n = k, \bf{\theta}) \\ &= \sum_{k=1}^{K} \pi_k \times p(x_n \mid z_n = k, \bf{\theta}) \end{align} $$
Hope that helps!
