The mixture of Gaussian distributions is defined as
$$
f(x; \mu, \sigma,\pi) = \sum_{i=1}^K \pi_i\,\mathcal{N}(x\mid\mu_i,\sigma_i)
$$
where $\mu = (\mu_1, \mu_2, \dots, \mu_K)$ is the vector or means, $\sigma = (\sigma_1, \sigma_2, \dots, \sigma_K)$ is the vector of variances, and $\pi = (\pi_1, \pi_2, \dots, \pi_K)$ is the vector of mixing proportions such that $\forall_i\,\pi_i \ge 0$ and $\sum_{i=1}^K \pi_i = 1$.
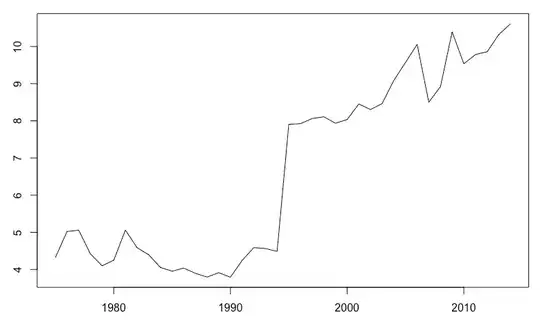
You didn't give us your code, but by just looking at the plot we can see that (a) the mixture components seem to be reasonably centered at the modes, and (b) the variances of the fitted normal distributions seem to be reasonably fitted to the data. The only thing that looks wrong, are the heights of the components. My guess is that when plotting the mixture, you plotted it with equal mixing weights $\pi_1 = \pi_2 = \dots = \pi_K = \tfrac{1}{K}$. Those mixing proportions make the individual components relatively "larger" or "smaller", since $\pi_i$ is the probability of observing $i$-th component, so this seems to be the case in here.
Below you can see example with proper mixing weights (red) and equal mixing weights (blue) in Gaussian mixture fitted to Galaxies dataset. As you can see, it looks as if it suffered from similar issues like your plot
import numpy as np
from matplotlib import pyplot as plt
from sklearn.mixture import GaussianMixture
from scipy.stats import norm
galaxies = np.array([
9172, 9350, 9483, 9558, 9775, 10227, 10406, 16084, 16170, 18419,
18552, 18600, 18927, 19052, 19070, 19330, 19343, 19349, 19440,
19473, 19529, 19541, 19547, 19663, 19846, 19856, 19863, 19914,
19918, 19973, 19989, 20166, 20175, 20179, 20196, 20215, 20221,
20415, 20629, 20795, 20821, 20846, 20875, 20986, 21137, 21492,
21701, 21814, 21921, 21960, 22185, 22209, 22242, 22249, 22314,
22374, 22495, 22746, 22747, 22888, 22914, 23206, 23241, 23263,
23484, 23538, 23542, 23666, 23706, 23711, 24129, 24285, 24289,
24366, 24717, 24990, 25633, 26690, 26995, 32065, 32789, 34279
])/1000
galaxies = galaxies.reshape((galaxies.shape[0], 1))
K = 6
def mix_pdf(x, loc, scale, weights):
d = np.zeros_like(x)
for mu, sigma, pi in zip(loc, scale, weights):
d += pi * norm.pdf(x, loc=mu, scale=sigma)
return d
mix = GaussianMixture(n_components=K, random_state=1, max_iter=100).fit(galaxies)
pi, mu, sigma = mix.weights_.flatten(), mix.means_.flatten(), np.sqrt(mix.covariances_.flatten())
grid = np.arange(np.min(galaxies), np.max(galaxies), 0.01)
plt.hist(galaxies, bins=20, density=True, alpha=0.2)
plt.plot(grid, mix_pdf(grid, mu, sigma, pi), label='varying weights')
plt.plot(grid, mix_pdf(grid, mu, sigma, [1./K]*K), label='equal weights')
plt.plot(galaxies, [0.01]*galaxies.shape[0], '|', color='k')
plt.legend(loc='upper right')
plt.show()