38

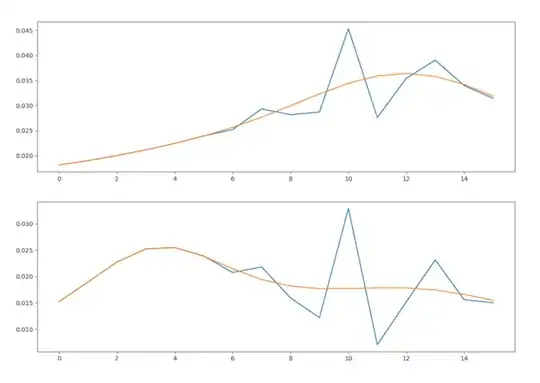
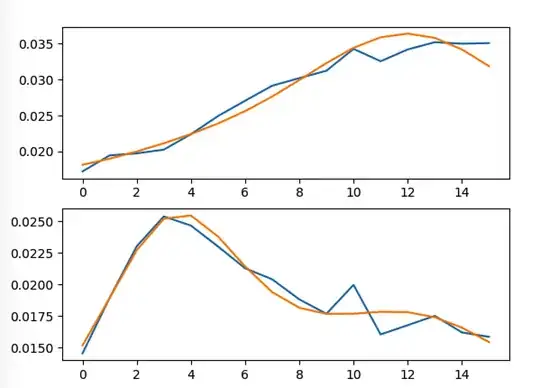
I was trying to learn machine learning using the Coursera material. In this lecture, Andrew Ng uses gradient descent algorithm to find the coefficients of the linear regression model that will minimize the error function (cost function).

For linear regression, do we need gradient descent? It seems I can analytically differentiate the error function and set it to zero to solve for the coefficients; is that right?

Tim
  • 108,699
  • 20
  • 212
  • 390
Victor
  • 5,925
  • 13
  • 43
  • 67
  • 3
    Linear models have been decently well handled since the 1700's. There are a ton of ways to handle them that don't require gradient descent (GD). There are nonlinear models where most of those methods fall flat on their face. Andrew is making you use an unfamiliar but very useful method against a very simple problem so you can debug your approach. When you are good with the method you can apply it to the stunningly nonlinear problems for which GD is the only method to get results. – EngrStudent Jul 06 '15 at 17:26
  • 12
    No, you don't have to use approaches like gradient descent (that's not the only optimization method, in any case). You can indeed analytically solve it, as you suggest; you differentiate with respect to each parameter, so you get one equation per parameter. But it's useful to solve simple problems that can be done other ways; if you know the answer already you can be sure when you're getting the right answer with gradient descent. – Glen_b Jul 06 '15 at 17:27
  • If the cost function is the usual quadratic ('distance') penalty, there is a closed form solution. However, gradient descent is generally much faster, that is why it is typically used. – meh Jul 06 '15 at 17:48
  • In addition, gradient descent can be used to find numerical solutions to problems that are analytically intractable. I would suspect that he uses gradient descent early on to get one used to it. I believe he then uses gradient descent with neural nets. Needless to say the neural net situation is more complicated. I think from a pedagogical situation, having seen them before, with linear models, gradient descent for use with neural nets seems more reasonable. – meh Jul 06 '15 at 17:51
  • 3
    Thanks for posting thet link to the Andre Ng videos I watched several. I already knew it, though not to this extreme, but it's scary to see what the vast majority of people "learning" optimization are learning, not to mention what at least some of them are learning about statistical computing. Gene Golub, THE pioneer in computing and using SVD, would be rolling over in his grave if he knew what is being taught now in his Stanford Computer Science Dept. The "funniest' video is https://www.youtube.com/watch?v=B3vseKmgi8E , which recommends and compares the 2 WORST algorithms for least squares. – Mark L. Stone Jul 31 '15 at 19:03
  • I just want to share a very good paper on ill-conditioning and least square regression. Few important things. - (1) Please note that ill-conditioning is also called (multi) **collinearity**, or **confounding** in statistics. - (2) Note that $Ax=b$ in linear algebra is expressed as $y=Xb$ in statistics, very confusing notation but they are "**identical**". - (3) The solution of $Ax=b$ is $x= (A^T A)^{-1} A^T b$, while the solution of $y=X b$ is $b=(X^T X)^{-1} X^T y$, assuming $A$ is a rectangular matrix. - (4) Note that $(A^T A)$ or $(X^T X)$ is known as the correlation or covariance matrix, d – Sangdon Jun 07 '19 at 14:43

3 Answers3

50

Linear Least squares can be solved by

0) Using high quality linear least squares solver, based on either SVD or QR, as described below, for unconstrained linear least squares, or based on a version of Quadratic Programming or Conic Optimization for bound or linearly constrained least squares, as described below. Such a solver is pre-canned, heavily tested, and ready to go - use it.

1) SVD, which is the most reliable and numerically accurate method, but also takes more computing than alternatives. In MATLAB, the SVD solution of the unconstrained linear least squares problem A*X = b is pinv(A) * b, which is very accurate and reliable.

2) QR, which is fairly reliable and numerically accurate, but not as much as SVD, and is faster than SVD. In MATLAB, the QR solution of the unconstrained linear least squares problem A*X = b is A\b, which is fairly accurate and reliable, except when A is ill-conditioned, i.e., has large condition number. A\b is faster to compute than pinv(A) * b, but not as reliable or accurate.

3) Forming the Normal equations (TERRIBLE from reliability and numerical accuracy standpoint, because it squares the condition number, which is a very bad thing to do) and

3a) solving by Cholesky Factorization (not good)

3b) explicitly inverting matrix (HORRIBLE)

4) Solving as a Quadratic Programming problem or Second Order Cone problem

4a) Solve using high quality Quadratic Programming software. This is reliable and numerically accurate, but takes longer than SVD or QR. However, it is easy to add bound or general linear constraints, or linear or quadratic (two norm) penalty or regularization terms to the objective function, and still solve the problem using Quadratic Programming software.

4b) Solve as a Second Order Cone problem using high quality Conic Optimization software. Remarks are the same as for Quadratic Programming software, but you can also add bound or general linear constraints and other conic constraints or objective function terms, such as penalty or regularization terms in various norms.

5) Solve using high quality general purpose nonlinear optimization software. This may still work well, but will in general be slower than Quadratic Programming or Conic Optimization software, and maybe not quite as reliable. However, it may be possible to include not only bound and general linear constraints, but also nonlinear constraints into the least squares optimization. Also, can be used for nonlinear least squares, and if other nonlinear terms are added to the objective function.

6) Solve using lousy general purpose nonlinear optimization algorithms --> DON'T EVER DO THIS.

7) Solve using THE WORST POSSIBLE general purpose nonlinear optimization algorithm there is, i.e., gradient descent. Use this only if you want to see how bad and unreliable a solution method can be If someone tells you to use gradient descent to solve linear least squares problems

7 i) Learn about statistical computing from someone who knows something about it

7 ii) Learn optimization from someone who knows something about it.

Mark L. Stone
  • 12,546
  • 1
  • 31
  • 51
  • Nice post, why you think that Cholesky is *not good* given your system is PD though? (and not with a ridiculous condition number) BTW, I think in you want to say (or add) the notion of generalised inverse (used mostly for educational purposes obviously) either at the "SVD" or the "explicitly inverting" point. – usεr11852 Jul 31 '15 at 15:40
  • You've already formed the Normal equations, and therefore squared the condition number. Cholesky is basically just LU for symmetric matrices. and that is not so robust, especially for ill-conditioned matrices, i.e., those having high condition number. – Mark L. Stone Jul 31 '15 at 15:47
  • Because forming the Normal equations squares the condition number, what starts out as a "non-ridiculous" condition number can be a "ridiculous" condition number after being squared. – Mark L. Stone Jul 31 '15 at 15:55
  • 3
    BTW, it's ridiculous how frequently matrices with very high condition numbers are generated, especially by the unwashed masses (i.e., the majority of people doing linear least squares, especially given the democratization in access), who are not attuned to it. – Mark L. Stone Jul 31 '15 at 16:06
  • I see why you say that. You are correct, that's why I was specific to note that this was "*given your system is PD*" so you do not need to do the $A^TA$. When working with covariance matrices the $L(D)L^T$'s are extremely handy. (MALTAB's `mldivide` does use $LL^T$ when $A$ is symmetric PD for example.) I fully agree with your last comment; I have seen the same phenomenon more times than I would like. (+1 in general, good post). – usεr11852 Jul 31 '15 at 17:14
  • Yes, I could have added Cholesky without forming Normal equations as an option (I only listed Cholesky as an option under form Normal equations). In that case, there would be no squaring of the condition number, but it would still be much less reliable than QR. I see no reason to ever use Cholesky for linear least squares ... unless you don't care about the answer, in which case you might as well just say the answer is the vector of zeros or maybe ones, save all the computing, and just chill. – Mark L. Stone Jul 31 '15 at 17:24
  • I use Cholesky all the time on covariance matrices, but not to solve least squares problems. But calculating and using the Cholesky factorization of a very ill-conditioned covariance matrix can be tricky business indeed. – Mark L. Stone Jul 31 '15 at 17:31
  • Agreed (mostly). Cholesky is fine for symmetric PD systems of linear least squares with semi-reasonable condition numbers. If it was as crap as you originally suggested it would not be used in MATLAB's `mldivide` for example. To that extend, one of the most popular regression methods for mixed effects data in R, `lmer` relies on (sparse)Cholesky too (through `CHOLMOD`). A very ill-conditioned matrix possibly would not pass as a PD system anyway. – usεr11852 Jul 31 '15 at 17:47
  • 1
    mldivide, i.e.. backslash, i.e., \ uses QR when m ~= n (least squares), as I stated in the 2nd sentence of my paragraph (2) above. You'd be surprised how much crap there is in MATLAB though - not just in the toolboxes, some of which are absolutely horrid, but to a lesser extent in some of the core functions as well. – Mark L. Stone Jul 31 '15 at 19:11
  • If $m \neq n$ then the system is not symmetric so $LL^T$ would inapplicable. When it comes to `mldivide` I strongly disagree about the *crap* characterisation. It is a very well-thought, documented and carefully implemented function. – usεr11852 Jul 31 '15 at 19:58
  • Let us [continue this discussion in chat](http://chat.stackexchange.com/rooms/26479/discussion-between-usr11852-and-mark-l-stone). – usεr11852 Jul 31 '15 at 19:58
  • 1
    @MarkL.Stone, great answer! could you please explain a bit more on why it's not advisable to use Gradient descent for solving least square! (in my understanding it's just an iterative approach compared to the others(direction solution approaches) which you have mentioned above). Moreover, Could you also comment on the problem: "if I have n>=30,000 features for a problem, Normal equation method will be very slow since inverting n*n matrix would be terrible! on the other hand, GD would work in this case pretty! any thoughts on how SVD & QR will perform". any suggestion would be helpful. – Anu Dec 28 '18 at 05:29
  • 1
    @ anu Only use gradient descent as a last resort. and that would only be if the problem is too big to be solved by SVD or QR. Never form the Normal Equations, let alone explicitly invert a matrix to solve Normal equations, NEVER. 30,000 features doesn't sound like very many for nowadays. – Mark L. Stone Dec 28 '18 at 17:17
  • What about successive orthogonalization using Gram Schmidt? I didn't see that listed, or are you embedding that with QR factorization? – 24n8 May 05 '21 at 18:00
  • @24n8 Per https://cran.r-project.org/web/packages/matlib/vignettes/gramreg.html , re: carrying out Gram-Schmidt process directly by successively projecting each successive variable on the previous ones and subtracting (taking residuals). "The QR method uses essentially the same process, factoring the matrix X as X=QR, where Q is the orthonormal matrix corresponding to Z and R is an upper triangular matrix. However, the signs of the columns of Q are arbitrary, and QR() returns QR(X)$Q with signs reversed, compared to Z." – Mark L. Stone May 05 '21 at 20:08
0

Finding coefficients of a linear model is technically the process of finding solutions to a set of Linear Equations.

For computing such solutions, a lot of optimization techniques have been developed and Gradient Descent is one of them.
Thus, Gradient Descent is not the only way to do that.

Andrew Ng uses it in the course is because it is simple to understand, without dealing with advanced Linear Algebra and Numerical Computing.

Vikas Raturi
  • 109
  • 2
  • While not wrong I think your answer misses the bigger picture by focusing on a non-standard case. The *vast majority* of linear regression models are fitted by using QR decomposition employing a closed form solution. `GD` -gradient decent- is used as an example to introduce more advanced methods (eg. `SGD` - stochastic `GD`). – usεr11852 Jul 31 '15 at 12:59
  • Can you elaborate what is QR decomposition? – Victor Jul 31 '15 at 14:08
  • 3
    You want to solve $Ax=b$. Given $A=QR$ where $R$ is upper triangular and $Q$ is orthogonal, $ Ax=b \Rightarrow QRx=b \Leftrightarrow Rx = Q^Tb$ which can be solved by backward substitution (ie. fast) as $R$ is triangular and $Q^T Q=I$. For *very large matrices* (millions of entries) this can be more expensive than an iterative solver eg. `SGD`. As most people do not have very large matrices the QR decomposition is better. In general QR decomposition has shaped the numerical world; [SIAM](https://www.siam.org/pdf/news/637.pdf) selected it as one of the top10 algorithms of the 20th century. – usεr11852 Jul 31 '15 at 14:26
  • @usεr11852 yes ofcourse. That because, i wanted to keep the answer simple, so as to avoid concepts such as QR decompostion, remaining relevant to the domain of Ng's course level. – Vikas Raturi Jul 31 '15 at 17:03
  • 4
    QR was one of the top 10 algorithms of the 20th century. But time marches on, and even though effective algorithms for computing SVD date back to the 1960s, you have to look at the importance of the application areas. Therefore I believe SVD is the TOP algorithm of the 21st century. Quite frankly, have you ever heard of QR being used to recommend movies? No, SVD is used for that critical appiication. SVD clearly is the algorithm of choice when Twitter sends out unsolicited recommendations to conservative old geezers as to which teenage celebrities they should follow. Let's see QR do that!!! – Mark L. Stone Jul 31 '15 at 17:41
-1

Yes you can.

To solve the Ax=B problem you can use the QR or other matrix decomposition based least squares solvers. However, I tried to do it by Gradient Descent with L2 norm regularization. And I think GD is better.

The first picture is the result of numpy.nnls, orange line is ground truth, blue line is numpy.nnls result.

The second picture is the result of my gradient descent with l2 norm result.

The second result is better.

numpy.nnls result

gradient descent

samson.wang
  • 1
  • 2
    In the second case you used regularization, so you optimized different functions, hence it tells nothing about comparing the optimization algorithms. – Tim Mar 04 '22 at 20:46