Mean Square Error and Gradient Descent

Question

I am trying to learn gradient descent and in the course of so I am trying to find the optimal m and c value for my model, for $y=mx+c$

For that, I have plotted the MSE using the below code in python

   #building the model

#lets start with random value of m and c

m=0
c=0

l=0.0001 #l is the learning rate


n=float(len(X_train)) # n=number of training data, we are converting it to float since we will need to divide n

mse=[]

for i in range (0,4000):
    Y_pred=m*X_train+c
    
    mse.append(numpy.sum((Y_train-Y_pred)**2)/n)
    D_m= (-2/n) * sum(X_train*(Y_train-Y_pred))
    D_c= (-2/n) * sum(Y_train-Y_pred)
    
    m=m-l*D_m
    c=c-l*D_c
   
 
    
plt.plot(mse)

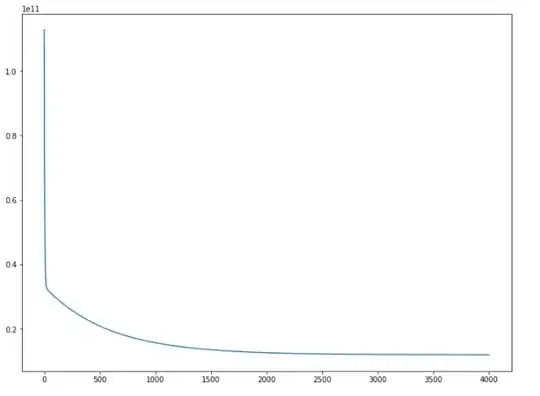
And the output I am getting for this is this-->

So it seems that the SME becomes more or less same after 2000, and remains more or less same till 4000

So I am taking m and c values that I have got in 4000th iteration. From the graph, we can see that the MSE value is lesser than 0.2.

But to my surprise when I do

mse[-1]

I get a HUGE NUMBER as Answer

The answer that I get for mse[-1] is 12041739532.188858

And for this reason, my final model performs absolutely worst, producing something like this as the output on the training set.

It will be very helpful if someone can guide me on why this is happening with the MSE value. Thank you.

score 1 · Accepted Answer · answered Aug 11 '20 at 16:58

1

Look at the scale of your graph. The vertical axis spans something like $10^{10}$ to $10^{11}$, as you can see by the 1e11 printed above the vertical scale. Your plot doesn't show that the error is below 0.2, it shows that the error is below 0.2e11.

This is consistent with the printed value for mse[-1].

answered Aug 11 '20 at 16:58

Sycorax

76,417
20
189
313

1

yeah, this is one of those instances where the way the default choices of the plotting package seem almost deliberately deceptive. – Sycorax Aug 11 '20 at 17:00
what should i do to converge the MSE much faster? increase the learning rate right? – Turing101 Aug 11 '20 at 17:01
I watched this here--> https://www.youtube.com/watch?v=4PHI11lX11I – Turing101 Aug 11 '20 at 17:05
@carlo, can u explain where it is wrong? – Turing101 Aug 11 '20 at 17:09
sorry, I made my computations by mind, but it seems your equations were right all along. that's strange, what is plotted in the second figure? – carlo Aug 11 '20 at 17:15
anyway, MSE is quadratic on the parameters, so, apart from analytic solution, best approach is adaptive GD, rather than simply a bigger learning rate – carlo Aug 11 '20 at 17:17
If you want to use gradient descent, then an analysis of the Hessian of the loss function will tell you how large you can make the learning rate without causing the optimization to diverge. This is explained in *Neural Networks Design *(2nd Ed.) Chapter 9 by Martin T. Hagan, Howard B. Demuth, Mark Hudson Beale, Orlando De Jesús. But if you don't care about the method used, then I suggest reading https://stats.stackexchange.com/questions/160179/do-we-need-gradient-descent-to-find-the-coefficients-of-a-linear-regression-mode/164164#164164 – Sycorax Aug 11 '20 at 17:20
using the hessian is the same as finding the solution analytically, since a quadratic function is completely determined by its first two derivatives – carlo Aug 11 '20 at 17:33
Using the Hessian to set the step size of a **gradient descent** method is emphatically not the same as solving the linear system directly, because the gradient descent method will likely take more than 1 step to reach the minimum. You can see a fully worked example in *Neural Network Design*. – Sycorax Aug 11 '20 at 17:41
if you use newton-rampson to solve linear regression you reach the solution in one step exactly. i don't know any other reasonable method to "use hessian to set the step size of a gradient descent" – carlo Aug 11 '20 at 17:57
@carlo First-order methods are very common, especially in neural networks; it seems quite reasonable to use a first-order method on OLS, even though other methods are available, because a student might be interested in learning how to apply gradient descent to a simple problem. Reading the book I've suggested would expand the methods that you *know*, but since your objections seems to turn on what you deem "reasonable," there doesn't seem to be anything profitable to be had by belaboring this point. – Sycorax Aug 11 '20 at 18:08
@Sycorax it is you that brought up hessian matrix, of course you wouldn't generally use it for NNs, there are two many parameters to compute the whole matrix, that's another reason for me suggesting adaptive GD – carlo Aug 11 '20 at 18:17
OP asked whether increasing the learning rate would help. I suggested how to find the largest learning rate that would work by using the Hessian. After that, I'm completely mystified. For some reason, you really want to talk about Newton's method. As far as I can tell, you've conflated any usage of the Hessian matrix with Newton's method. This isn't true, and even though Newton is more efficient, it doesn't have anything to do with how to choose the learning rate for gradient descent. I don't know why you're so adamant about this, but whatever is at issue here, I don't think it's statistical. – Sycorax Aug 11 '20 at 18:41
1

Guys figured out at last why it was giving such weird values. I haven't feature scaled my data. That is why it was acting like this after feature scaling everything is working fine as expected. – Turing101 Aug 12 '20 at 06:01

Mean Square Error and Gradient Descent

1 Answers1