I would like to test if they are distributed according to an exponential distribution. I can apply the Kolmogorov-Smirnov in python using scipy.stats.kstest(data, 'expon') .
However, I assume I have to normalize my data somehow first. Otherwise it is comparing it with an exponential distribution with unknown rate $\lambda$. Is this right and how should I do that?
You can standardize the exponential distribution easily enough multiplying variates by the rate parameter (it's a reciprocal scale parameter). But if you're estimating the rate parameter from the data, the Kolmogorov–Smirnov statistic doesn't have the same distribution as when the exponential distribution is completely specified.
See Lilliefors (1969), "On the Kolmogorov–Smirnov tests for the exponential distribution with mean parameters", JASA, 64, 325. And https://stats.stackexchange.com/a/392686/17230 for an intuitive explanation of the phenomenon in general.
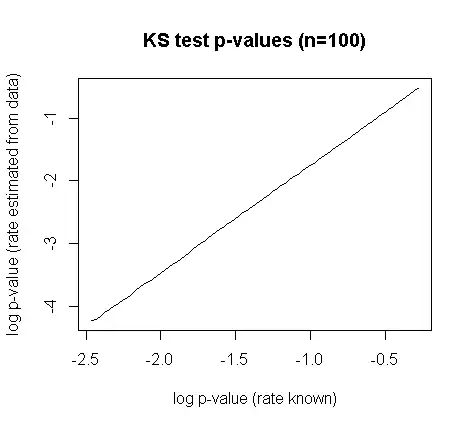
You can compare the observed value of the KS test statistic calculated from the data to the tabulated critical values given in the reference. Or simulate the distribution of the statistic yourself as @Glen_b & @soakley have suggested. Note that Lilliefors points out its distribution doesn't depend on the true values of the parameters—generally true for scale & location parameters—, so for a given sample size you can do this once simulating from the standard exponential distribution, & keep the results for future reference; you don't need to repeat the simulation for each new data-set of the same sample size. And there's therefore no approximation involved (except that coming from simulation error). The difference made to the distribution of the KS statistic $D$ by estimating rather than pre-specifying the parameters is not trivial:
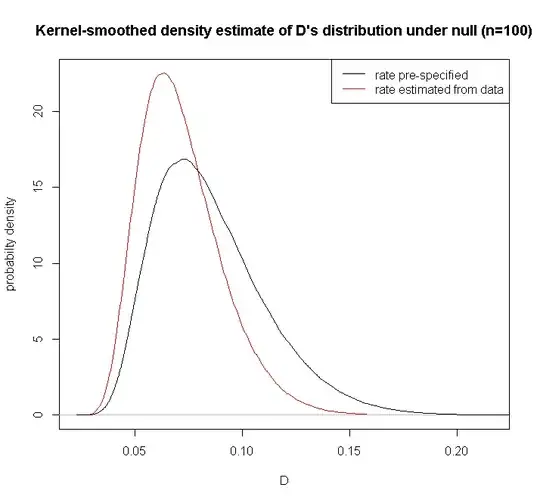
Lilliefors does give some asymptotic results (worked out rather crudely, but good enough for government work). Stephens has tabulated quantiles for the modified statistic
$$T(n) = \left(D - \frac{0.2}{n}\right)\left(\sqrt{n} + 0.26 + \frac{0.5}{\sqrt{n}}\right)$$
where $D$ is the KS test statistic & $n$ the sample size. According to Durbin (1975), "Kolmogorov–Smirnov tests when parameters are estimated with applications to tests of exponentiality and tests on spacings", Biometrika, 62, 1, these are very close to the exact values for larger sample sizes. They can be found in Pearson & Hartley (1972), Biometrika Tables for Statisticians, CUP, or in Stephens (1974), "EDF Statistics for goodness of fit and some comparisons", JASA, 69, 347. I'm not aware of any published correction to the p-value of the ordinary KS test to approximate that of the Lilliefors test; a power-law relationship seems like it might be useful:
You don't need to normalize, but can get the p-value for a goodness-of-fit test by simulation. Here is some sample R code, taken from Greg Snow's answer to a similar question (KS test - R, Minitab (and Systat)):
data <- c(7.2,10.5,10.67,0.15,3.92,3.28,0.89,2.29,13.82,0.43)
simp <- replicate(100000, {x <- rexp(length(data),rate=1/mean(data));
ks.test(x,"pexp",rate=1/mean(x))$p.value} )
mean(simp <= ks.test(data,"pexp",1/mean(data))$p.value)
The method is described by Clauset et. al in a SIAM paper "Power-Law Distributions in Empirical Data."
No, you don't need to normalise your data since the KS statistic is defined in terms of the raw data (actually in terms of the empirical distribution of these data):
http://en.wikipedia.org/wiki/Kolmogorov%E2%80%93Smirnov_test#Kolmogorov.E2.80.93Smirnov_statistic
I don't know Python, but in R you can conduct this test as follows:
x = rexp(100,1)
ks.test(x,"pexp",1)
For this purpose, and by construction, you need to know the parameters of the distribution. You should not plug estimators in it, this breaks the convergence of the statistic and you have to use a different test (see the wikipedia article).
If you want to estimate the parameters and check whether the fitted model is good, then what you actually need is a goodness of fit test, for which you have a variety of options:
