I am testing the set of data of coefficient J. It looks like this
I want to test the normality of this set using the K-S test, but I.m not sure how the parameters should be adjusted here. I wrote
from scipy.stats import kstest
seed(1234)
# normality test
result = kstest(J_ridge.flatten(), 'norm',alternative='greater')
>> KstestResult(statistic=0.49068097451020654, pvalue=0.0)
But I don't know what alternative to use or other parameters needed in the K-S test.
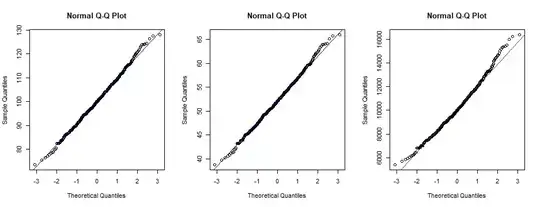
Perhaps a more useful test of normality, if $\mu$ and $\sigma$ are unknown, would be the Shapiro-Wilk test.
The null hypothesis of the Kolmogorov-Smirnov test is that the population from which data are sampled has a specific normal distribution (with specified mean $\mu$ and and standard deviation $\sigma.)$ Consequently, if you used a K-S test, you would need to estimate $\mu \approx \bar X = \frac{1}{n}\sum_{i=1}^n X_i$ and $\sigma^2 \approx S^2= \frac{1}{n-1}\sum_{i=1}^n (X_i-\bar X)^2,$ but you would have to allow for that estimation in determining the P-value of the K-S test.
By contrast, the null hypothesis of the Shapiro-Wilk test is that the population from which data are randomly sampled is some normal distribution (with unspecified parameters). Another advantage is that the S-W test has better power (is more likely to detect actual non-normality) for a given sample size.
Example in R:
Sample of size $n=500$ from $\mathsf{Norm}(\mu=100, \sigma=10):$
set.seed(831)
x = rnorm(500, 100, 10)
summary(x); length(x); sd(x)
Min. 1st Qu. Median Mean 3rd Qu. Max.
73.63 94.31 100.08 100.30 106.79 127.85
[1] 500 # sample size
[1] 9.575485 # sample standard deviation
The null hypothesis is not rejected at the 5% level; P-value 0.674. So data $X$ are 'consistent with normal'.
shapiro.test(x)
Shapiro-Wilk normality test
data: x
W = 0.99754, p-value = 0.674
Linear transformation of $X$ changes parameters, but $Y$ still passes the normality test (P-value unchanged).
y = .5*x + 2
summary(y); length(y); sd(y)
Min. 1st Qu. Median Mean 3rd Qu. Max.
38.81 49.16 52.04 52.15 55.39 65.93
[1] 500
[1] 4.787742
shapiro.test(y)$p.val
[1] 0.6739557
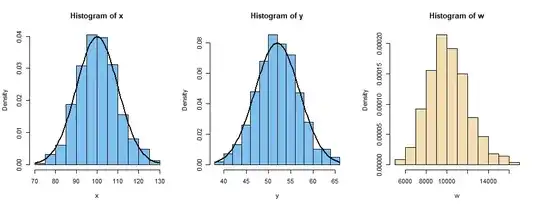
Nonlinear transformation, destroys normality. S-W test rejects normality for $W$ (P-value below 5%).
summary(w); length(w); sd(w)
Min. 1st Qu. Median Mean 3rd Qu. Max.
5421 8895 10016 10151 11404 16347
[1] 500
[1] 1935.915
shapiro.test(w)$p.value
[1] 0.001056042
Graphical displays:
The histogram of $W$ is right-skewed, not normal.
The normal quantile plot of $W$ (right panel) is distinctly nonlinear.
