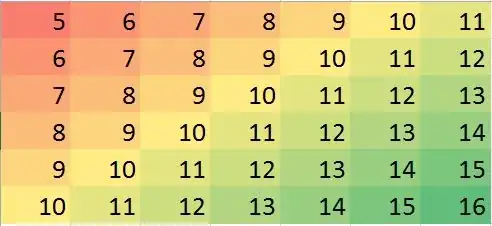
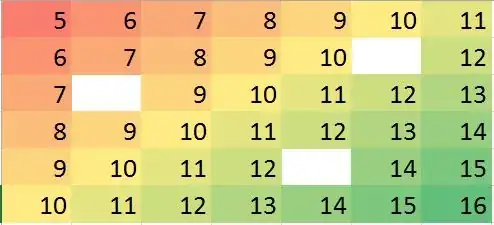
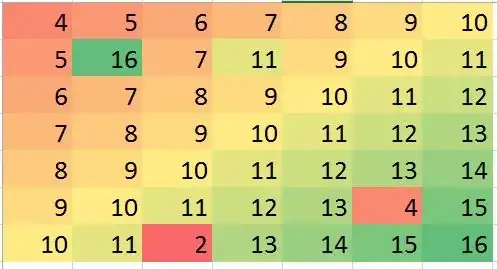
The question asks for ways to use nearest neighbors in a robust way to identify and correct localized outliers. Why not do exactly that?
The procedure is to compute a robust local smooth, evaluate the residuals, and zero out any that are too large. This satisfies all the requirements directly and is flexible enough to adjust to different applications, because one can vary the size of the local neighborhood and the threshold for identifying outliers.
(Why is flexibility so important? Because any such procedure stands a good chance of identifying certain localized behaviors as being "outlying". As such, all such procedures can be considered smoothers. They will eliminate some detail along with the apparent outliers. The analyst needs some control over the trade-off between retaining detail and failing to detect local outliers.)
Another advantage of this procedure is that it does not require a rectangular matrix of values. In fact, it can even be applied to irregular data by using a local smoother suitable for such data.
R, as well as most full-featured statistics packages, has several robust local smoothers built in, such as loess. The following example was processed using it. The matrix has $79$ rows and $49$ columns--almost $4000$ entries. It represents a complicated function having several local extrema as well as an entire line of points where it is not differentiable (a "crease"). To slightly more than $5\%$ of the points--a very high proportion to be considered "outlying"--were added Gaussian errors whose standard deviation is only $1/20$ of the standard deviation of the original data. This synthetic dataset thereby presents many of the challenging features of realistic data.
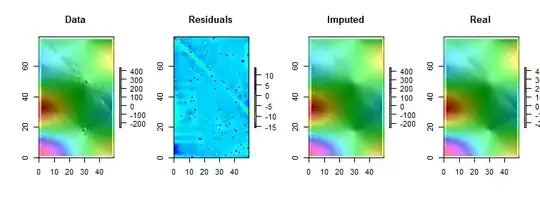
Note that (as per R conventions) the matrix rows are drawn as vertical strips. All images, except for the residuals, are hillshaded to help display small variations in their values. Without this, almost all the local outliers would be invisible!
By comparing the "Imputed" (fixed up) to the "Real" (original uncontaminated) images, it is evident that removing the outliers has smoothed out some, but not all, of the crease (which runs from $(0,79)$ down to $(49, 30)$; it is apparent as a light cyan angled stripe in the "Residuals" plot).
The speckles in the "Residuals" plot show the obvious isolated local outliers. This plot also displays other structure (such as that diagonal stripe) attributable to the underlying data. One could improve on this procedure by using a spatial model of the data (via geostatistical methods), but describing that and illustrating it would take us too far afield here.
BTW, this code reported finding only $102$ of the $200$ outliers that were introduced. This is not a failure of the procedure. Because the outliers were Normally distributed, about half of them were so close to zero--$3$ or less in size, compared to underlying values having a range of over $600$--that they made no detectable change in the surface.
#
# Create data.
#
set.seed(17)
rows <- 2:80; cols <- 2:50
y <- outer(rows, cols,
function(x,y) 100 * exp((abs(x-y)/50)^(0.9)) * sin(x/10) * cos(y/20))
y.real <- y
#
# Contaminate with iid noise.
#
n.out <- 200
cat(round(100 * n.out / (length(rows)*length(cols)), 2), "% errors\n", sep="")
i.out <- sample.int(length(rows)*length(cols), n.out)
y[i.out] <- y[i.out] + rnorm(n.out, sd=0.05 * sd(y))
#
# Process the data into a data frame for loess.
#
d <- expand.grid(i=1:length(rows), j=1:length(cols))
d$y <- as.vector(y)
#
# Compute the robust local smooth.
# (Adjusting `span` changes the neighborhood size.)
#
fit <- with(d, loess(y ~ i + j, span=min(1/2, 125/(length(rows)*length(cols)))))
#
# Display what happened.
#
require(raster)
show <- function(y, nrows, ncols, hillshade=TRUE, ...) {
x <- raster(y, xmn=0, xmx=ncols, ymn=0, ymx=nrows)
crs(x) <- "+proj=lcc +ellps=WGS84"
if (hillshade) {
slope <- terrain(x, opt='slope')
aspect <- terrain(x, opt='aspect')
hill <- hillShade(slope, aspect, 10, 60)
plot(hill, col=grey(0:100/100), legend=FALSE, ...)
alpha <- 0.5; add <- TRUE
} else {
alpha <- 1; add <- FALSE
}
plot(x, col=rainbow(127, alpha=alpha), add=add, ...)
}
par(mfrow=c(1,4))
show(y, length(rows), length(cols), main="Data")
y.res <- matrix(residuals(fit), nrow=length(rows))
show(y.res, length(rows), length(cols), hillshade=FALSE, main="Residuals")
#hist(y.res, main="Histogram of Residuals", ylab="", xlab="Value")
# Increase the `8` to find fewer local outliers; decrease it to find more.
sigma <- 8 * diff(quantile(y.res, c(1/4, 3/4)))
mu <- median(y.res)
outlier <- abs(y.res - mu) > sigma
cat(sum(outlier), "outliers found.\n")
# Fix up the data (impute the values at the outlying locations).
y.imp <- matrix(predict(fit), nrow=length(rows))
y.imp[outlier] <- y[outlier] - y.res[outlier]
show(y.imp, length(rows), length(cols), main="Imputed")
show(y.real, length(rows), length(cols), main="Real")