Short version
Is there a difference per treatment given time and this dataset?
Or if the difference we're trying to demonstrate is important, what's the best method we have for teasing this out?
Long version
Ok, sorry if a bit biology 101 but this appears to be an edge case where the data and the model need to line up in the right way in order to draw some conclusions.
Seems like a common issue... Would be nice to demonstrate an intuition rather than repeating this experiment with larger sample sizes.
Let's say I have this graph, showing mean +- std. error:
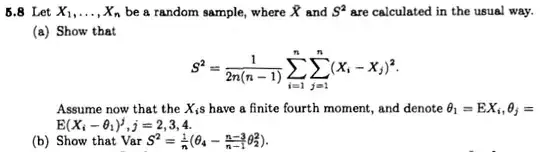
Now, it looks like there's a difference here. Can this be justified (avoiding Bayesian approaches)?
The simpleminded man's approach would be to take Day 4 and apply a t-test (as usual: 2-sided, unpaired, unequal variance), but this doesn't work in this case. It appears the variance is too high as we only had 3x measurements per time-point (err.. mostly my design, p = 0.22).
Edit On reflection the next obvious approach would be ANOVA on a linear regression. Overlooked this on first draft. This also doesn't seem like the right approach as the usual linear model is impaired from heteroskedasticity (exaggerated variance over time). End Edit
I'm guessing there's a way to include all the data which would fit a simple (1-2 parameter) model of growth over time per predictor variable then compare these models using some formal test.
This method should be justifiable yet accessible to a relatively unsophisticated audience.
I have looked at compareGrowthCurves in statmod, read about grofit and tried a linear mixed-effects model adapted from this question on SE. This latter is closest to the bill, although in my case the measurements are not from the same subject over time so I'm not sure mixed-effects/multilevel models are appropriate.
One sensible approach would be to model the rate of growth per time as linear and fixed and have the random effect be Tx then test it's significance, although I gather there's some debate about the merits of such an approach.
(Also this method specifies a linear model which would not appear to be the best way to model a comparison of growth which in the case of one predictor has not yet hit an upper boundary and in the other appears basically static. I'm guessing there's a generalized mixed-effects model approach to this difficulty which would be more appropriate.)
Now the code:
df1 <- data.frame(Day = rep(rep(0:4, each=3), 2),
Tx = rep(c("Control", "BHB"), each=15),
y = c(rep(16e3, 3),
32e3, 56e3, 6e3,
36e3, 14e3, 24e3,
90e3, 22e3, 18e3,
246e3, 38e3, 82e3,
rep(16e3, 3),
16e3, 34e3, 16e3,
20e3, 20e3, 24e3,
4e3, 12e3, 16e3,
20e3, 5e3, 12e3))
### standard error
stdErr <- function(x) sqrt(var(x)) / sqrt(length(x))
library(plyr)
### summarise as mean and standard error to allow for plotting
df2 <- ddply(df1, c("Day", "Tx"), summarise,
m1 = mean(y),
se = stdErr(y) )
library(ggplot2)
### plot with position dodge
pd <- position_dodge(.1)
ggplot(df2, aes(x=Day, y=m1, color=Tx)) +
geom_errorbar(aes(ymin=m1-se, ymax=m1+se), width=.1, position=pd) +
geom_line(position=pd) +
geom_point(position=pd, size=3) +
ylab("No. cells / ml")
Some formal tests:
### t-test day 4
with(df1[df1$Day==4, ], t.test(y ~ Tx))
### anova
anova(lm(y ~ Tx + Day, df1))
### mixed effects model
library(nlme)
f1 <- lme(y ~ Day, random = ~1|Tx, data=df1[df1$Day!=0, ])
library(RLRsim)
exactRLRT(f1)
this last giving
simulated finite sample distribution of RLRT. (p-value based on 10000
simulated values)
data:
RLRT = 1.6722, p-value = 0.0465
By which I conclude that the probability of this data (or something more extreme), given the null hypothesis that there is no influence of treatment on change over time is close to the elusive 0.05.
Again, sorry if this appears a bit basic but I feel a case like this could be used to illustrate the importance of modelling in avoiding further needless experimental repetition.