0

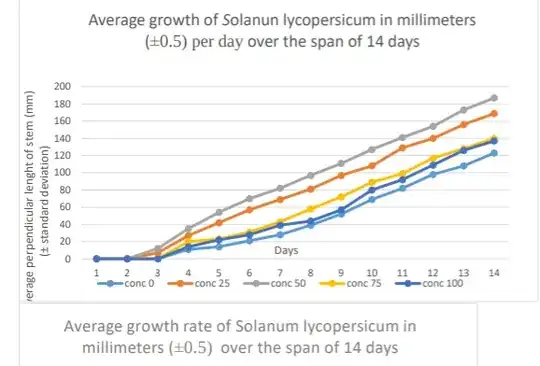
I am doing a biology experiment about the effects of 5 different concentrations (0%,25%, 50%, 75%, and 100%) on plant growth. It was a 5×5 trial. From 0% to 50% my plant's height increased, with 50% being the highest. But from 50% to 100% my plants' height began to decrease or grew at a slower rate almost as slow as the 0%.

Before the experiment took place, I hypothesized that an increase in concentration will lead to an increase in growth in my plants. I planned to do an ANOVA one-way test. But given my data, I intend to do 2 ANOVA one-way test. (This is because I feel that one ANOVA test is more suitable when the data follows either an upward or downward trend, not both.) The first one for the 0% to 50%, do check for the statistical significance of the upward trend and the second one for 50% to 100% to check for the statistical significance of the downward trend.

Do you think this is the right thing to do?
Which statistical test is more suitable? enter image description here

Maria E. Onambele
  • 1
  • 1
  • 1
    I think you need to investigate regression and add in terms which are non-linear in concentration. Dividing up your data-set in a data-dependent way makes all your significance levels and confidence intervals lose their normal meaning. – mdewey Oct 10 '20 at 14:16
  • Search this site for [tag:growth-model]. – kjetil b halvorsen Oct 11 '20 at 02:25

1 Answers1

1

You have repeated measurements data, and should fit a growth model. There will probably be some kind of serial correlation you should take into account. Your two factors seems to be time and concentration, you could try a polynomial in time. There are many similar posts here you can use as examples, for instance Do statisticians assume one can't over-water a plant, or am I just using the wrong search terms for curvilinear regression? and Demonstrate difference in growth over time, Which random effects to include in this GLMM?

Now that you have included a plot of the growth curves in the post: Apart from the first few days (where everything is $\approx 0$), the curves are quite parallel. But note that the two curves with slowest growth correspond to maximum and minimum concentration. You could try to fit a linear mixed-effects model, with random intercepts.

kjetil b halvorsen
  • 63,378
  • 26
  • 142
  • 467