Jarque-Bera normality test in R

Question

Jarque-Bera normality test has significant p-values even when there is skewness and kurtosis. Does that mean test is infering data distribution is approximately normal?

Answer 1

You may have misunderstood something about hypothesis testing or maybe about goodness-of-fit tests, or perhaps specifically about the "Jarque-Bera" test*.

Note that you reject when the p-value is small, when happens when the skewness and kurtosis differ from their expected values under normality.

The test statistic is of the form (from page 1 of Bowman and Shenton's paper):

$$\frac{n}{6} S^2 + \frac{n}{24} (K-3)^2\,,$$

where $S$ is the sample skewness and $K$ is the sample kurtosis (i.e. $K-3$ is 'excess kurtosis')

The null hypothesis is of normality, and rejection of the hypothesis (because of a significant p-value) leads to the conclusion that the distribution from which the data came is non-normal.

The test is specifically looking for skewness and kurtosis that is different from that of the normal (it squares the standardized deviations and sums them) and will tend to be significant when skewness and kurtosis deviating from the values at the normal are present.

Which is to say - when you get a significant test statistic with this test, it's explicitly because the sample skewness or kurtosis (or both) are different from what you expect to see with a sample from normal distribution.

Take care, however -- the asymptotic approximation on which the test is based comes in only very slowly (see the image near the bottom of this answer; also see here and here for some additional points). I wouldn't rely on it without simulating the distribution of the test statistic unless $n$ is a good deal larger than say 100.

Here's an example of the joint distribution in normal samples at n=30 (simulated values):

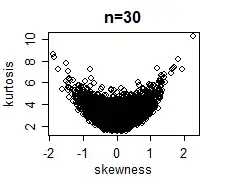
-- as you see, not at all close to bivariate normal.

---

*(The development of the test precedes their 1980 paper; it shouldn't be named for them. D'Agostino & Pearson (1973), and then Bowman & Shenton (1975) were there well before for example, and the latter discussed the relevant issues in more detail (including the slow convergence and the shape of the joint distribution in small samples - though their diagrams seem as if they may contain an error), but one can readily see that the idea of basing a goodness of fit test on skewness and kurtosis together comes even earlier than those prior papers.)