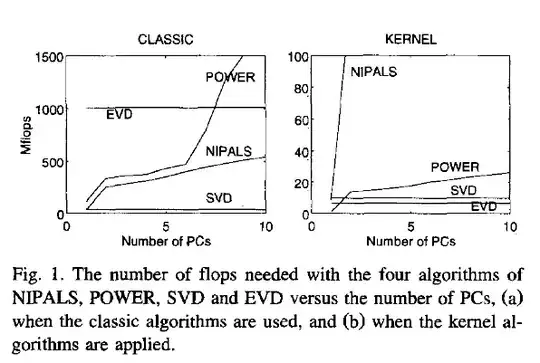
SVD is slower but is often considered to be the preferred method because of its higher numerical accuracy.
As you state in the question, principal component analysis (PCA) can be carried out either by SVD of the centered data matrix $\mathbf X$ (see this Q&A thread for more details) or by the eigen-decomposition of the covariance matrix $\frac{1}{n-1}\mathbf X^\top \mathbf X$ (or, alternatively, $\mathbf{XX}^\top$ if $n\ll p$, see here for more details).
Here is what is written in the MATLAB's pca() function help:
Principal component algorithm that pca uses to perform the principal component analysis [...]:
'svd' -- Default. Singular value decomposition (SVD) of X.
'eig' -- Eigenvalue decomposition (EIG) of the covariance matrix. The EIG algorithm is faster than SVD when the number of observations, $n$, exceeds the number of variables, $p$, but is less accurate because the condition number of the covariance is the square of the condition number of X.
The last sentence highlights the crucial speed-accuracy trade-off that is at play here.
You are right to observe that eigendecomposition of covariance matrix is usually faster than SVD of the data matrix. Here is a short benchmark in Matlab with a random $1000\times 100$ data matrix:
X = randn([1000 100]);
tic; svd(X); toc %// Elapsed time is 0.004075 seconds.
tic; svd(X'); toc %// Elapsed time is 0.011194 seconds.
tic; eig(X'*X); toc %// Elapsed time is 0.001620 seconds.
tic; eig(X*X'); toc; %// Elapsed time is 0.126723 seconds.
The fastest way in this case is via the covariance matrix (third row). Of course if $n \ll p$ (instead of vice versa) then it will be the slowest way, but in that case using the Gram matrix $\mathbf{XX}^\top$ (fourth row) will be the fastest way instead. SVD of the data matrix itself will be slower either way.
However, it will be more accurate because multiplying $\mathbf X$ with itself can lead to a numerical accuracy loss. Here is an example, adapted from @J.M.'s answer to Why SVD on $X$ is preferred to eigendecomposition of $XX^⊤$ in PCA on Math.SE.
Consider a data matrix $$\mathbf X = \begin{pmatrix}1&1&1\\\epsilon & 0 & 0\\ 0 & \epsilon & 0 \\ 0 & 0 & \epsilon\end{pmatrix},$$ sometimes called Läuchli matrix (and let us omit centering for this example). Its squared singular values are $3+\epsilon^2$, $\epsilon^2$, and $\epsilon^2$. Taking $\epsilon = 10^{-5}$, we can use SVD and EIG to compute these values:
eps = 1e-5;
X = [1 1 1; eye(3)*eps];
display(['Squared sing. values of X: ' num2str(sort(svd(X),'descend').^2')])
display(['Eigenvalues of X''*X: ' num2str(sort(eig(X'*X),'descend')')])
obtaining identical results:
Squared sing. values of X: 3 1e-10 1e-10
Eigenvalues of X'*X: 3 1e-10 1e-10
But taking now $\epsilon = 10^{-10}$ we can observe how SVD still performs well but EIG breaks down:
Squared sing. values of X: 3 1e-20 1e-20
Eigenvalues of X'*X: 3 0 -3.3307e-16
What happens here, is that the very computation of covariance matrix squares the condition number of $\mathbf X$, so especially in case when $\mathbf X$ has some nearly collinear columns (i.e. some very small singular values), first computing covariance matrix and then computing its eigendecomposition will result in loss of precision compared to direct SVD.
I should add that one is often happy to ignore this potential [tiny] loss of precision and rather use the faster method.