How can I sample from a mixture distribution, and in particular a mixture of Normal distributions in R? For example, if I wanted to sample from:
$$ 0.3\!\times\mathcal{N}(0,1)\; + \;0.5\!\times\mathcal{N}(10,1)\; + \;0.2\!\times\mathcal{N}(3,.1) $$
how could I do that?
It's good practice to avoid for loops in R for performance reasons. An alternative solution which exploits the fact rnorm is vectorized:
N <- 100000
components <- sample(1:3,prob=c(0.3,0.5,0.2),size=N,replace=TRUE)
mus <- c(0,10,3)
sds <- sqrt(c(1,1,0.1))
samples <- rnorm(n=N,mean=mus[components],sd=sds[components])
In general, one of the easiest ways to sample from a mixture distribution is the following:
Algorithm Steps
1) Generate a random variable $U\sim\text{Uniform}(0,1)$
2) If $U\in\left[\sum_{i=1}^kp_{k},\sum_{i=1}^{k+1}p_{k+1}\right)$ interval, where $p_{k}$ correspond to the the probability of the $k^{th}$ component of the mixture model, then generate from thedistribution of the $k^{th}$ component
3) Repeat steps 1) and 2) until you have the desired amount of samples from the mixture distribution
Now using the general algorithm given above, you could sample from your example mixture of normals by using the following R code:
#The number of samples from the mixture distribution
N = 100000
#Sample N random uniforms U
U =runif(N)
#Variable to store the samples from the mixture distribution
rand.samples = rep(NA,N)
#Sampling from the mixture
for(i in 1:N){
if(U[i]<.3){
rand.samples[i] = rnorm(1,0,1)
}else if(U[i]<.8){
rand.samples[i] = rnorm(1,10,1)
}else{
rand.samples[i] = rnorm(1,3,.1)
}
}
#Density plot of the random samples
plot(density(rand.samples),main="Density Estimate of the Mixture Model")
#Plotting the true density as a sanity check
x = seq(-20,20,.1)
truth = .3*dnorm(x,0,1) + .5*dnorm(x,10,1) + .2*dnorm(x,3,.1)
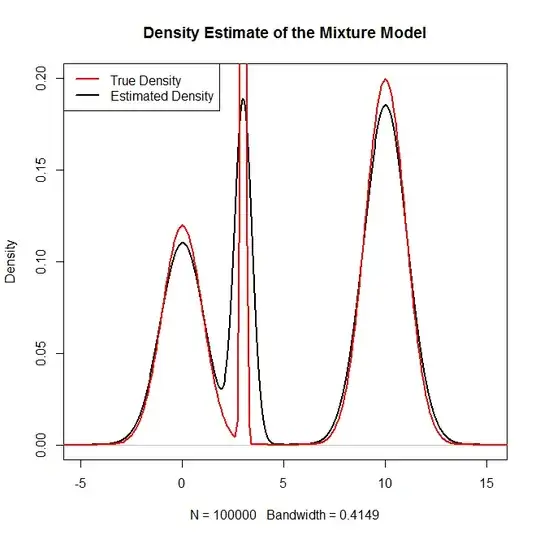
plot(density(rand.samples),main="Density Estimate of the Mixture Model",ylim=c(0,.2),lwd=2)
lines(x,truth,col="red",lwd=2)
legend("topleft",c("True Density","Estimated Density"),col=c("red","black"),lwd=2)
Which generates:
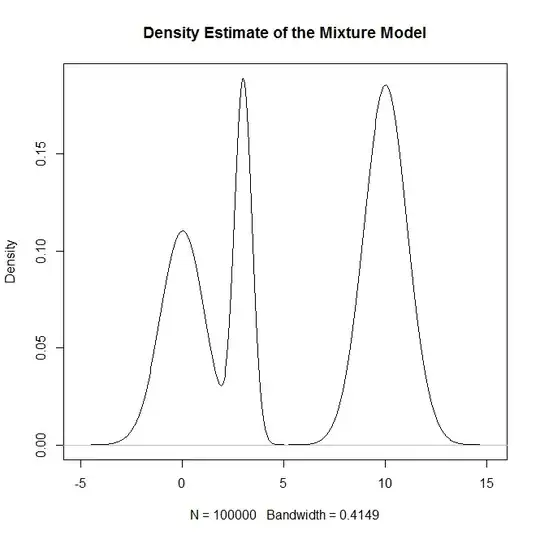
and as a sanity check:
Conceptually, you are just picking one distribution (from $k$ possibilities) with some probability, and then generating pseudo-random variates from that distribution. In R, this would be (e.g.):
set.seed(8) # this makes the example reproducible
N = 1000 # this is how many data you want
probs = c(.3,.8) # these are *cumulative* probabilities; since they
# necessarily sum to 1, the last would be redundant
dists = runif(N) # here I'm generating random variates from a uniform
# to select the relevant distribution
# this is where the actual data are generated, it's just some if->then
# statements, followed by the normal distributions you were interested in
data = vector(length=N)
for(i in 1:N){
if(dists[i]<probs[1]){
data[i] = rnorm(1, mean=0, sd=1)
} else if(dists[i]<probs[2]){
data[i] = rnorm(1, mean=10, sd=1)
} else {
data[i] = rnorm(1, mean=3, sd=.1)
}
}
# here are a couple of ways of looking at the results
summary(data)
# Min. 1st Qu. Median Mean 3rd Qu. Max.
# -3.2820 0.8443 3.1910 5.5350 10.0700 13.1600
plot(density(data))
Already given perfect answers, so for those who want to achieve this in Python, here is my solution:
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
mu = [0, 10, 3]
sigma = [1, 1, 1]
p_i = [0.3, 0.5, 0.2]
n = 10000
x = []
for i in range(n):
z_i = np.argmax(np.random.multinomial(1, p_i))
x_i = np.random.normal(mu[z_i], sigma[z_i])
x.append(x_i)
def univariate_normal(x, mean, variance):
"""pdf of the univariate normal distribution."""
return ((1. / np.sqrt(2 * np.pi * variance)) *
np.exp(-(x - mean)**2 / (2 * variance)))
a = np.arange(-7, 18, 0.01)
y = p_i[0] * univariate_normal(a, mean=mu[0], variance=sigma[0]**2) + p_i[1] * univariate_normal(a, mean=mu[1], variance=sigma[0]**2)+ p_i[2] * univariate_normal(a, mean=mu[2], variance=sigma[0]**2)
fig, ax = plt.subplots(figsize=(8, 4))
ax.hist(x, bins=100, density=True)
ax.plot(a, y)
