How can I generate a random variable which follows the mixture Gaussian distributions:
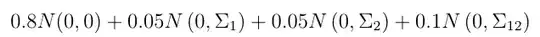
I found the answer and tried to simulate it, but I think it is not the right dataset I wanted.
Here is my code:
M = 100
sigma1 = matrix(c(0.2, 0, 0, 0),ncol=2)
sigma2 = matrix(c(0, 0, 0, 0.4),ncol=2)
sigma12 = matrix(c(0.2, 0.028, 0.028, 0.4),ncol=2)
U = runif(M)
b = cbind(rep(NA,M),rep(NA,M))
for (i in 1:M) {
if (U[i]<.8) {
b[i,] = c(0,0)
} else if (U[i]<.85) {
b[i,] = rmvnorm(1,sigma = sigma1)
} else if (U[i]<.9) {
b[i,] = rmvnorm(1,sigma = sigma2)
} else {
b[i,] = rmvnorm(1,sigma = sigma12)
}
}
Is there something wrong? Thanks in advance!