I'm looking for the best approach to and/or methods of solving the following inference problem. I have tried searching for similar questions but don't have enough knowledge on the various methods (variational inference, SVI, MCMC, HMC, MLE, particle filtering, ... etc.) to know which are relevant to this problem. Any help categorizing methods and their applicability would be very much appreciated.
The model of the system is a combination of a simple discrete random variable (a sequence of Bernoulli trials) with continuous random noises and a discrete-time dynamic model (a simple integrator in this example although it could be any transfer function).
The goal is to estimate the parameters of this random shock model, given the model structure and a sequence of output measurements which are noisy (to represent measurement errors).
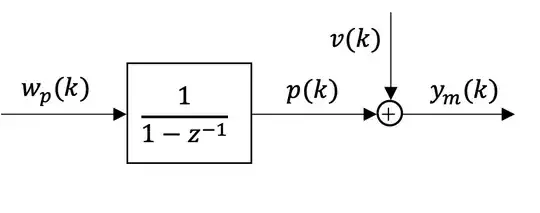
Process model:
where $\frac{1}{1-z^{-1}}$ is a transfer function and $w_{p}(k)$ is a 'random shock' variable defined as:
$$ w_{p}(k) \sim \begin{cases} \mathcal{N}(0, \sigma_{w_p}^2) & \text{with probability } 1-\epsilon \\ \mathcal{N}(0, b^2 \sigma_{w_p}^2) & \text{with probability } \epsilon \end{cases} $$
the disturbance signal $p(k)$ is generated using:
$$p(k)=\frac{1}{1-z^{-1}}w_{p}(k)$$
and the measurement model is:
$$ v(k) \sim \mathcal{N}(0, \sigma_{M}^2)$$
or (equivalently):
$$ y_m(k) \sim \mathcal{N}(p(k), \sigma_{M}^2)$$
The following plot shows what the measured output might look like:
The goal is to estimate $\epsilon$, and $b\sigma_{w_p}$ (which are assumed to be time invariant) from a sufficiently long sequence of observations. We can assume that $\sigma_{M}$ is known.
As far as I understand it, this is not a trivial problem because it is a sequential decision-making problem (i.e. recursive) and so the system output at time $k$ is dependent on all previous inputs, and furthermore, the random shock variable $w_p(k)$ is not Gaussian (it is a mixture of two Gaussians). So I believe an approximate method or numerical approach is required, which is what lead me to SVI initially.
I verified that stochastic variational inference (SVI) can be used if $w_{p}$ were measurable as I demonstrate here but I do not know if this approach will still work in the (recursive) case where only $y_m(k)$ is measured.
Reference:
- MacGregor, J.F., Harris, T.J., and Wright, J.D. (1984). Duality Between the Control of Processes Subject to Randomly Occurring Deterministic Disturbances and ARIMA Stochastic Disturbances. Technometrics, 26(4), 389–397.