2

I have been meaning to fit an exponential smoothing model to a monthly series that looks like the one below: enter image description here

When I decompose the series it is almost evident that we have seasonality and also there seems to be an exponential trend in the series. Here is the result: enter image description here

I first used ets function to apply it on my training set and the diagnostic was an ETS model with additive error, but neither seasonality nor trend:

fit2 <- ets(training)
fit2

ETS(A,N,N) 

Call:
 ets(y = training) 

  Smoothing parameters:
    alpha = 0.4596 

  Initial states:
    l = 354.3194 

  sigma:  155.3593

     AIC     AICc      BIC 
365.3796 366.4231 369.2672

And the Ljung-Box test also looks fine:

fit2 %>% checkresiduals()

    Ljung-Box test

data:  Residuals from ETS(A,N,N)
Q* = 2.235, df = 3, p-value = 0.5251

Model df: 2.   Total lags used: 5

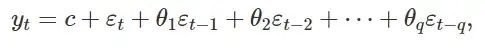
When I plot the forecasts for 4 months ahead, it seems to be a straight line, as the model doesn't capture the dynamics of the series: enter image description here

Now I have 2 questions:

  • Do I need to detrend & deseaonalize the times series with lag 1 and lag 12 differencing before applying an ets model on it. Because I heard from Mr. Hyndman on a datacamp tutorial that we just have to plug in the series into ets so, I am a bit confused here. If I use HoltWinter function I will get a different result, but I don't know the difference between these two.
  • Do this model seems legitimate and correct? I am not sure why it could not capture the dynamics here but since there is a seamingly polynomial trend here I thought that might lead to ets diagnose the trend to N, but what about seasonality? why it cannot be catpured?

Thank you very much for your advice in advance I really appreciate it.

Richard Hardy
  • 54,375
  • 10
  • 95
  • 219
Anoushiravan R
  • 223
  • 7
  • 1
    Does your series have a unit root or a seasonal unit root? If not, why would you consider taking lag 1 or lag 12 differences? That would introduce a unit-root moving-average component and double (taken together, quadruple) your error variance. Briefly, removing a deterministic trend and/or non-unit-root seasonality by differencing is a bad idea. – Richard Hardy Dec 03 '21 at 18:36
  • Thank you very much for your reply Mr. Hardy. I am afraid I don't know yet how to discern if my series have a unit root for example. Could you please let me know how I could detect that? – Anoushiravan R Dec 03 '21 at 18:39
  • 1
    You could eyeball and you could apply a unit root test and a seasonal unit root test. Looking at the graph, I do not see a unit root in your series. Regarding tests, see e.g. the help file for the `auto.arima` function from the `forecast` package in R. But if your series is short (say, under 40 observations for the unit root test and under $40m$ observations for the seasonal unit root test with a seasonal frequency $m$ – these are *very* rough numbers), the formal tests will be of limited use. I would trust eyeballing more than test results for short series. – Richard Hardy Dec 03 '21 at 18:41
  • I used `ndiffs` function for this and the result of `kpss` and `pp` were `0`, while the result of `adf` was `1`. So do we actually have seasonality here and if so why the model don't capture it? I also try to fit other models as well. Just wanted to understand the diagnostic here. – Anoushiravan R Dec 03 '21 at 18:46
  • 1
    The tests you mention do not deal with seasonality. Again, with a series as short as yours it is no wonder the ADF test cannot reject the null of a unit root. But I got you right, the KPSS test cannot reject stationarity either. Looking at the graph, I would bet on stationarity. – Richard Hardy Dec 03 '21 at 19:02
  • So no wonder why `ets` function chose `ets(A,N,N)` as the best fit here, if I am not wrong. Thank you very much for your response Mr. Hardy :) I really appreciate it. – Anoushiravan R Dec 03 '21 at 19:10

1 Answers1

2

Do I need to detrend & deseasonalize the times series with lag 1 and lag 12 differencing before applying an ets model on it?

Does your series have a unit root or a seasonal unit root? If not, why would you consider taking lag 1 or lag 12 differences? (Eyeballing your series does not suggest that.) Each would introduce a unit-root moving-average component into your process and increase your error variance (the first would double it, the other I am not sure by how much). In general, removing a deterministic trend and/or non-unit-root seasonality by differencing is not a good idea.

Richard Hardy
  • 54,375
  • 10
  • 95
  • 219
  • Thank you for your message. Since I am very new to this field, I still don't understand why despite the `decompose` result we don't have seasonality here? is it because of the fact the series is short then? and if so is it the reason why the forecast values are just a straight line? – Anoushiravan R Dec 03 '21 at 19:28
  • 1
    @AnoushiravanR, you may or may not have actual seasonality. Its estimated pattern may be strong or weak. If it is weak, modelling it might introduce more variance in your forecasts than it would reduce bias in them, so it would be detrimental. If it is strong, go ahead and model it using dummy variables, Fourier terms, SARIMA or any other technique. Just think twice before (seasonally) differencing a series that does not have a (seasonal) unit root. – Richard Hardy Dec 03 '21 at 19:32
  • Oh my god, I understand now. I got the function wrong now I used `nsdiffs` and applied `seas` and `ocsb` tests and they both returned `0`. So based on the documentation since the seasonality strength exeeds `0.64` maybe we should apply differencing. But I guess `ets` can detect it automatically. As is the case with `auto.arima` too. – Anoushiravan R Dec 03 '21 at 19:49
  • 1
    If `nsdiffs` returned 0 then I suppose you do not need to difference. And let me reiterate: only a very special case of seasonality requires differencing. A strong seasonal pattern does not require (or even warrant) seasonal differencing *unless there is a unit root component there* (which is rarely the case in my experience and which the plot of your series does not seem to suggest). – Richard Hardy Dec 03 '21 at 20:28
  • I don't know how to thank you for all the valuable points this past week. I am going to work on this subject for my thesis, so I think I will explore forecasting methods in depth to get a better understanding as I am very naive right now. But I am so happy that I have this opportunity to learn from contributors with vast experience. – Anoushiravan R Dec 03 '21 at 22:50
  • 1
    @AnoushiravanR, I am here for the fun of learning and helping others learn. No worries, your words are a great form of thanking me. Good luck with your project! – Richard Hardy Dec 04 '21 at 08:05
  • Thank you very much Mr. Hardy, that's very kind of you. I can relate to what you mentioned as I am doing the same thing on stackoverflow, but sometimes it gets very addictive and I have scale myself back. – Anoushiravan R Dec 04 '21 at 11:14