In problems like this it is important that you read specifically which information is given to you and which is the problem. So let's start with assignment 1.
The probability that Andrew is still alive - let's call that $P(A)$ and the probability that Ellen is still alive is $P(B)$.
What we are looking for is the event that both are still alive, so both events occur simultaneously, which we call $A \cap B$.
As noted, they tell you these events are independent. That means:
By definition, the probability of this event is
$P(A \cap B) = P(A) * P(B) $
So one of your question was, how is this related to the Venn diagramme?
Well, independence is not readily apparent in the venn diagramm. A Venn diagramme needs to look a certain way if there is independence, but even if it looks that way you only know events are independent if the problem set tells you! This is a bit tricky but stay with me.
If you'd draw a Venn diagramme for this first exercise, you would see that:
$$P(A \cap B) / P(A) = P(B) / 1$$
Which is the same as
$$P(A \cap B) / P(A) = P(B) / P(\Omega)$$
In essence that means that the chance of "hitting" $B$ if you are already in $A$ is the same as the chance of hitting $B$ in the first place - or said differently - no matter if you hit $A$ - the chance of hitting $B$ is always the same.
If $P(A)$ was 0,5, then the probability of $A \cap B$ would have to be 50% of the size of $A$.
Only then can the events be independent.
Try to draw this up, it is a nice exercise.
Also - are you aware that if the size of $A \cap B$ is zero in the Venn diagramme, then the events can not be independent? Think about why.
From this point on maybe you want to draw Venn diagramms as you follow along.
Okay so far so good. Now let's see what about problem two?
Well firstly, note that these events are not independent. You are, in fact, given given the probability that both lights are red at the same time and this probability does not fit what you know about independence.
For you to see the difference to the first example, let us see what can happen at that intersection.
We want to know when both lights are green. What is the complement of this event? It's NOT "both lights are red". In fact the two complementary events are:
- Both lights are green
- At least one light is red
It is either option 1 or 2. Option 1 is what we are after. If we can figure out the probability of option 2, then we know that option 1 is the complement/opposite of it, right? So let's figure out event 2.
Okay so why is there another probability given in the assignment? Well think about it: Event 2 can be described differently.
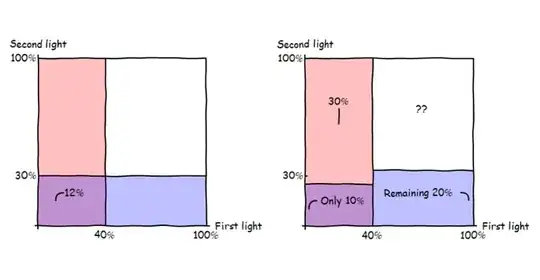
- The first light can be red, let us call this $A$
- The second light can be red, let's call this one $B$
Okay so this is probably where you are right now. The probabilities for these two events, let's call them $P(A)$ and $P(B)$ are given: $.4$ and $.3$
We also know:
- The first and the second light are red at the same this - this is $A \cap B$ : $.1$
How does this fit together?
Well $A$ and $B$ are not enough to calculate when both lights are green (event 1), because we will need the second event - which we called: "Either light is red" and then take its complement (you already figured this out).
Now - why can we not multiply the probabilities? First: because they are not independent. The multiplication rule can not be used because the ratio of $A \cap B$ to either $A$ or $B$ is not as it was in the first example.
Second: Because even if they were independent, then multiplication gives us the event $A \cap B$ - the event that both occur at the same time. But we want the event that either light is red.
Let's think about how this event can also be described.
The name you are looking for is $A \cup B$.
What does it include?
$A \cup B = $
-Light $A$ can be red AND light $B$ can be red. We will call this $A \cap B$ (we have this!)
-Light $A$ can be red and light $B$ can be green. This is called $A \cap \neg B$
-Light $A$ can be green and light $B$ can be red. This is called $\neg A \cap B$
(the $\neg$ means negation or complement)
So the problem is we have $A$ and $B$ and $A \cap B$, but not the probabilities for either light beeing red, while the other is green, $A \cap \neg B$ and $\neg A \cap B$
To make this short, here is where you apply the additive rule.
You can easily see why if you look at your Venn diagramms. The difference between $A$ and $A \cap \neg B$ is what?
Well it's the part of the intersection, $A \cap B$ which is in $A$.
The same goes for $B$. So if we add $A$ and $B$ instead of $(A \cap \neg B)$ and $(\neg A \cap B)$, we have added two things too much. First: the part of the intersection that lies in $A$ and second: the part of the intersection that lies in $B$.
Go ahead and draw this in your circles.
What you want to see is: What is the difference between $$A+B$$ and $$(A \cup B) = (A \cap B) + (A \cap \neg B) + (\neg A \cap B)$$ ?
Well the difference is exactly one time the intersection. So to get the probability of our event "At least one light is red", all we need to do is to add $P(A)$ and $P(B)$ and substract the intersect $P(A \cap B)$ and we have $$P(A) + P(B) - P(A \cap B) = P(A \cup B)$$
Alright and this is the same as "At least one light is red". And what's the opposite of this? It's "Both lights are green" - the solution to the problem.