Question Restatement and Generalisation
$A$, $B$, and $C$ are binary unknowns whose possible values are $0$ and $1$. Let $Z_i$ stand for the proposition, "The value of $Z$ is $i$". Also let $(X | Y)$ stand for "The probability that $X$, given that $Y$". What is $(A_a | B_b C_c I)$, given that
- $(A_{a_1} | B_{b_1} I) = u_1$ and $(A_{a_2} | C_{c_2} I) = u_2$
- $(A_{a_1} | B_{b_1} I) = u_1$ and $(A_{a_2} | C_{c_2} I) = u_2$ and $(B C | I) = (B | I)(C | I)$
- $(A_{a_1} | B_{b_1} I) = u_1$ and $(A_{a_2} | C_{c_2} I) = u_2$ and $(A_0 | I) = \frac{1}{2}$
- $(A_{a_1} | B_{b_1} I) = u_1$ and $(A_{a_2} | C_{c_2} I) = u_2$ and $(A_0 | I) = \frac{1}{2}$ and $(B C | I) = (B | I)(C | I)$
and that $I$ contains no relevant information besides what is implicit in the assignments? The last conjunct of conditions 2 and 4 is shorthand for the independence statement
$$
(B_j C_k | I) = (B_j | I)(C_k | I) \quad , \quad j = 0, 1 \quad k = 0,1
$$
Treat each of the four cases in turn.
Answers
Case 1
We have to specify the distribution $(ABC | I)$. The problem is underdetermined, because $(ABC | I)$ requires eight numbers, but we have only three equations---the two given conditions and the normalisation condition.
It has been shown by various esoteric means that the distribution to assign when the information doesn't otherwise determine a solution is the one that, of all distributions consistent with the known information, has the greatest entropy. Any other distribution implies that we know more than the known information, which of course is a contradiction.
All we need to do, therefore, is assign the maximum entropy distribution. This is more easily said than done, and I have not found a general closed-form solution. But particular solutions can be found using a numerical optimiser. We maximise
$$
- \sum_{i,j,k} (A_i B_j C_k | I) \ln (A_i B_j C_k | I)
$$
subject to the constraints
$$
\sum_{i,j,k} (A_i B_j C_k | I) = 1
$$
and
$$
(A_{a_1} | B_{b_1} I) = u_1 \quad\quad \text{i.e.} \quad \frac{\sum\limits_k (A_{a_1} B_{b_1} C_k | I )}{\sum\limits_{i,k} (A_i B_{b_1} C_k | I)} = u_1
$$
and
$$
(A_{a_2} | C_{c_2} I) = u_2 \quad\quad \text{i.e.} \quad \frac{\sum\limits_j (A_{a_2} B_j C_{c_2} | I)}{\sum\limits_{i,j} (A_i B_j C_{c_2} | I)} = u_2
$$
Now let's apply this to the question. If we have
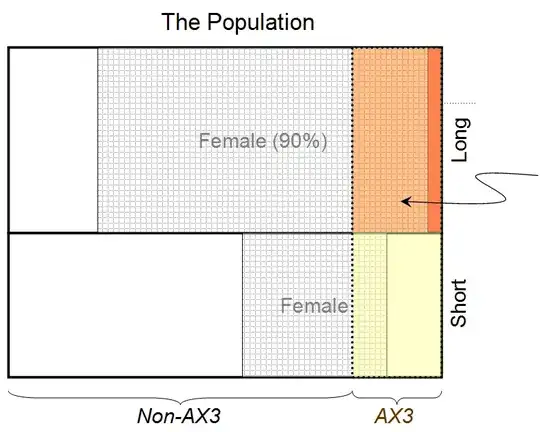
- "The person is female" $\longleftrightarrow A_1$
- "The person has long hair" $\longleftrightarrow B_1$
- "The person has blood type AX3" $\longleftrightarrow C_1$
then $a = 1$, $b = 1$, $c = 1$, $a_1 = 1$, $b_1 = 1$, $a_2 = 1$, $c_2 = 1$, $u_1 = 0.9$, $u_2 = 0.8$, and we find that for the maximum entropy solution, $(A_1 | B_1 C_1 I) \simeq 0.932$. Therefore the probability that the person behind the curtain is female, given that he/she has long hair and blood type AX3, is 0.932.
Case 2
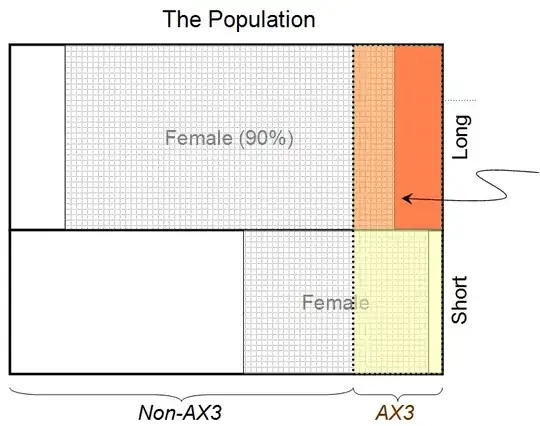
Now we repeat the exercise with the extra constraint that for a given person, knowing the value of $B$ (the hair state) does not affect our estimate of the value of $C$ (the blood type state), and vice versa. Everything is the same as in Case 1, except there are two extra constraints in the optimisation, namely:
\begin{align*}
(B_0 | C_l I) &= (B_0 | I) \quad , \quad l = 0, 1 \\
\end{align*}
i.e.
\begin{align*}
\frac{\sum\limits_i (A_i B_0 C_l | I)}{\sum\limits_{i,j} (A_i B_j C_l | I)} &= \sum_{i,k} (A_i B_0 C_k | I) \quad , \quad l = 0, 1
\end{align*}
This gives $(A_1 | B_1 C_1 I) \simeq 0.936$, so the probability that the person behind the curtain is female, given that he/she has long hair and blood type AX3, is 0.936.
Case 3
Now we remove the independence condition and replace it with the prior condition that there is an equal chance that a given person is male or female:
$$
(A_0 | I) = \frac{1}{2} \quad \quad \text{i.e.} \quad \sum_{j,k} (A_0 B_j C_k | I) = \frac{1}{2}
$$
This time $(A_1 | B_1 C_1 I) \simeq 0.973$, so the probability that the person behind the curtain is female, given that he/she has long hair and blood type AX3, is 0.973.
Case 4
Finally we reintroduce the independence constraints of Case 2, and find that $(A_1 | B_1 C_1 I) \simeq 0.989$. Therefore the probability that the person behind the curtain is female, given that he/she has long hair and blood type AX3, is 0.989.