9

There is a significant 3-way interaction in a data-set I'm working with.

The interaction involves both categorical and quantitative variables.

I have been pointed towards simple slopes and this website but I find the explanations lacking. I only have a basic background in statistics, and Googling for other examples has not been very helpful.

Any insight as to how to begin to understand this interaction will be very welcome, especially using R rather than SPSS. Thank you very much in advance, from a lower-year college student who has suddenly found himself over his head!

chl
  • 50,972
  • 18
  • 205
  • 364
Stephen
  • 91
  • 1
  • 1
  • 2
  • 3
    Welcome to the site! Is one of the predictors categorical and the other two continuous, or the other way around? How many factor levels do the categorical variables have? Do you have an OLS problem or something more exotic? With this info, we may be able to point you to good ways to graph the interaction, which always helps in understanding. – Stephan Kolassa Jan 08 '13 at 22:12
  • 1
    Some information about the data could help, because it might suggest some approaches. In some cases the interaction is best modeled directly but in other cases it can be made to disappear via nonlinear re-expressions of the explanatory variables. – whuber Jan 08 '13 at 23:55
  • Thanks for the comments. There is one binary predictor, and two continuous. I think the answer to your 3rd question, Stephan, is that I'm doing a basic linear regression (if that's not what you were asking about, sorry, and could you please clarify!). – Stephen Jan 11 '13 at 04:20
  • Thanks for the update -- as you worked out from Stephan's note, OLS is about model fitting for linear regression (stands for Ordinary Least Squares) [cc @StephanKolassa] – James Stanley Jan 11 '13 at 06:14

3 Answers3

9

I was afraid this was going to be a continuous $\times$ continuous $\times$ categorical interaction... OK, here goes - first, we create some toy data (foo is a binary predictor, bar and baz are continuous, dv is the dependent variable):

set.seed(1)
obs <- data.frame(foo=sample(c("A","B"),size=100,replace=TRUE),
  bar=sample(1:10,size=100,replace=TRUE),
  baz=sample(1:10,size=100,replace=TRUE),
  dv=rnorm(100))

We then fit the model and look at the three-way interaction:

model <- lm(dv~foo*bar*baz,data=obs)
anova(update(model,.~.-foo:bar:baz),model)

Now, for understanding the interaction, we plot the fits. The problem is that we have three independent variables, so we would really need a 4d plot, which is rather hard to do ;-). In our case, we can simply plot the fits against bar and baz in two separate plots, one for each level of foo. First calculate the fits:

fit.A <- data.frame(foo="A",bar=rep(1:10,10),baz=rep(1:10,each=10))
fit.A$pred <- predict(model,newdata=fit.A)
fit.B <- data.frame(foo="B",bar=rep(1:10,10),baz=rep(1:10,each=10))
fit.B$pred <- predict(model,newdata=fit.B)

Next, plot the two 3d plots side by side, taking care to use the same scaling for the $z$ axis to be able to compare the plots:

par(mfrow=c(1,2),mai=c(0,0.1,0.2,0)+.02)
persp(x=1:10,y=1:10,z=matrix(fit.A$pred,nrow=10,ncol=10,byrow=TRUE),
  xlab="bar",ylab="baz",zlab="fit",main="foo = A",zlim=c(-.8,1.1))
persp(x=1:10,y=1:10,z=matrix(fit.B$pred,nrow=10,ncol=10,byrow=TRUE),
  xlab="bar",ylab="baz",zlab="fit",main="foo = B",zlim=c(-.8,1.1))

Result:

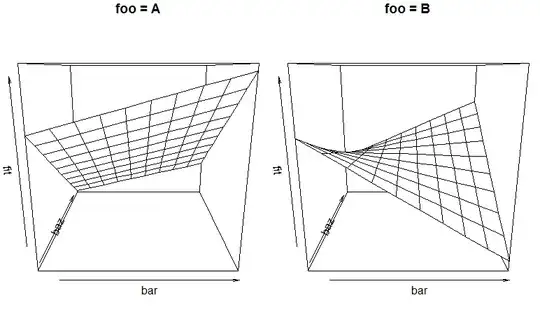
three way interaction

We see how the way the fit depends on (both!) bar and baz depends on the value of foo, and we can start to describe and interpret the fitted relationship. Yes, this is hard to digest. Three-way interactions always are... Statistics are easy, interpretation is hard...

Look at ?persp to see how you can prettify the graph. Browsing the R Graph Gallery may also be inspirational.

Stephan Kolassa
  • 95,027
  • 13
  • 197
  • 357
  • 2
    You can avoid the z-scaling issue and juxtaposition of the two subplots using `lattice` and its `wireframe()` function which let you write formula like `y ~ x1 * x2 | x3` to get a trellis display. – chl Jan 11 '13 at 22:13
  • +1 I like this approach. In essence, a three way interaction is illustrating that the shape of the "plane" (not a technically correct term, but close enough) -- as described by the two continuous predictors (bar and baz in this example) and the fitted outcome -- depends on the level of the grouping variable (foo in this example.) – James Stanley Jan 14 '13 at 02:30
  • Another thing -- If the interaction between the two continuous variables is being treated as linear, then the shape of each "plane" is somewhat constrained? (so you can't end up with seemingly crazy 3-d contours, with weird minima and maxima, in either of the two figures) – James Stanley Jan 14 '13 at 02:31
  • @JamesStanley: exactly. The plane will have the form $z=ax+by+cxy$ with different coefficients $a, b, c$ for each level of the grouping variable. This is indeed very much constrained. If we included higher powers (better: orthogonal polynomials) in the original model, we would end up with $x^jy^k$ terms here, and the shape of the fits could become a lot wilder. – Stephan Kolassa Jan 14 '13 at 09:53
3

+1 to comments above about graphing interaction.

An initial approach to thinking about a three-way interaction is that it is saying that the pattern of results contained in the interaction between A and B depends upon the level/value of C. The following is framed in a linear regression kind of framework, but conceptually similar to e.g. logistic regression.

This assumes that you're happy with thinking about two-way interactions, of course :-)

Let's say there are three predictors, A (continuous), B (categorical), and C (categorical).

A two way A*B interaction would indicate that the slope of A (relating to the outcome) depends on the level of B to which an individual belongs.

In this context, a three way A*B*C interaction would indicate that the A*B interaction (previously discussed differential slopes of A on the outcome according to group of B) depends on the group of C to which one belongs...

Things are much more complex if there are two continuous/ordinal predictors in the interaction (usually too complex to conceptualise: I would be interested to hear others' opinions on this.)

James Stanley
  • 2,376
  • 20
  • 32
  • 1
    I personally find even two-way interactions between two continuous predictors very hard to understand and interpret - factor $\times$ continuous is much easier. And ordinal (non-interval scaled) predictors should properly speaking not be in an ANOVA at all, since an ordinal predictor with values 1, 2, 3, ... will intrinsically be treated as a continuous predictor (which it shouldn't be if it is not interval scaled) - or, if we treat it as a factor, we lose the ordinality. Usually one treats such predictors (Likert scales and the like) as continuous, anyway. – Stephan Kolassa Jan 09 '13 at 07:56
  • Thanks for additional note on interval scaled data. I must admit I was still only thinking of two-way continuous predictor interaction complexity myself! Usually it's hard to make any (a priori) sense of what such an interaction might mean anyway that I don't think I've ever (really) attempted to model one. – James Stanley Jan 09 '13 at 20:19
  • Thanks for the conceptualization! I do generally understand 2-way interactions but you have certainly helped de-fuzz my understanding of a 3-way. If you think you could venture to shed some light on one with two continuous predictors I'm sure it would be even more helpful, since that's the kind I have to deal with right now :) – Stephen Jan 11 '13 at 04:23
1

Often it helps to plot the relationships and see how things change when you change one of the variables. A couple of tools in R that help with these plots are Predict.Plot and TkPredict functions in the TeachingDemos package.

Greg Snow
  • 46,563
  • 2
  • 90
  • 159