4

I have 214 covariates and a binary outcome. The total number of positive and negative outcomes is 27 and 33, respectively.

I already modelled it using a 1v1 univariable logistic regression and I found some significative coefficients.

After that I moved to a simple LASSO shrinkage and I obtained

> fit <- glmnet(x = fitXData, y = fitYData, family = "binomial", alpha = 1, nlambda = 50)

      Call:  glmnet(x = fitXData, y = fitYData, family = "binomial", alpha = 1, nlambda = 50) 

         Df   %Dev   Lambda
   [1,]  0 8.067e-16 0.156700
   [2,]  2 1.804e-02 0.142700
   [3,]  3 3.901e-02 0.129900
   [4,]  4 5.950e-02 0.118200
   [5,]  5 7.772e-02 0.107600
  ....

Now let's assume that I want to use a model composed with the two most significative covariates provided by lasso and to compare it with the real outcome. Being a binary outcome I wrote

>table(fitYData,predict(fit, s=0.142700, newx= fitXData, type="class"))

fitYData FALSE
 FALSE     33
  TRUE     27

meaning that the prediction is FALSE for all the outcomes.

Chosing a different lambda (see later for the specific value) i obtain better results:

> table(fitYData,predict(fit, s=0.05574419, newx= fitXData, type="class"))

fitYData FALSE TRUE
   FALSE    29    4
   TRUE     10   17

Clearly it's due to the fact that the big "lambda" (0.1427) chosen to remove the 212 less significative covariates strongly impacts (lower) the "beta"s predictors resulting in a fully negative prediction.

It seems a very common behaviour to me for big lambda values (for instance, see https://www.rstatisticsblog.com/data-science-in-action/lasso-regression/, before the section Sharing the R Squared formula, all the values are underestimated) but nobody mentions it.

Point 1:

Should I perform and ordinary glm fit including only the two variables I selected or should I blindly trust on the glmnet prediction for this big lambda?

Point 2:

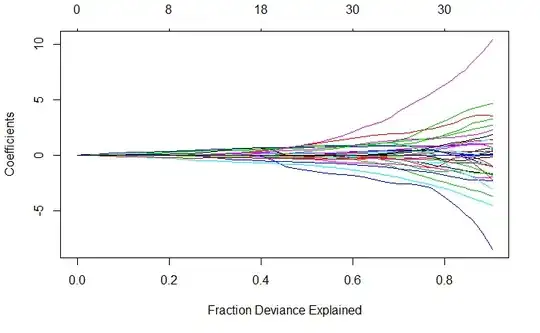
It seems to me that the correlation with the outcome is so small that it's very difficult to extract a good piece of information from it. I report the LASSO plot:

plot(fit, xvar = "dev")

Lasso Plot

And zooming: Zoomed Lasso Plot

The plot is not as clear as the ones I find in the online examples and papers... Is it normal?

Point 3:

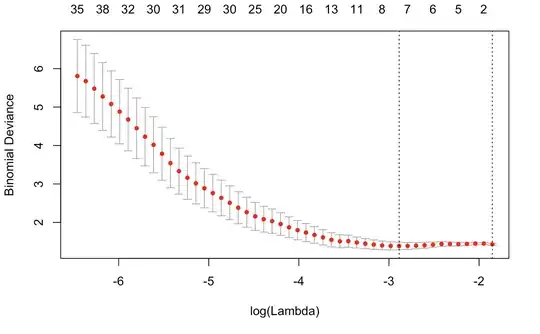
I also performed a CV Lasso with a leave-one-out k-fold: 

cvfit <- cv.glmnet(fitXData, fitYData, family="binomial", grouped=FALSE, type.measure = "deviance", nfold = 60, nlambda = 50)

CV results

I report the CV results:

cvfit\$lambda.min = 0.05574419

cvfit\$lambda.1se = 0.1567398

With lambda.min 8 covariates has been "selected" but with lambda.1se all the variables are rejected.

Again, is it due to the low intrinsic correlation/high noise or am I mistaking? Shouldn't the deviance increase for big lambdas? The usual trend of this last graph is usually the opposite...

Thank you for your help!! :)

Best regards. Giulio

Steffen Moritz
  • 1,564
  • 2
  • 15
  • 22
Giulio Benetti
  • 83
  • 5
  • So where is the issue? Don't select that lambda value, it is clearly crap. You could try to build a similar glm model with the selected variables by LASSO, but it won't be the same, since LASSO also does regularization. – user2974951 Aug 26 '19 at 13:13
  • 2
    Can you include the results for the cross-validated glm model? It might help us answer the question better if you do. The cv.glmnet output usually gives you a suggested lambda values (min and 1se) based on smallest cross-validation error. – Samir Rachid Zaim Aug 26 '19 at 13:58
  • @SamirRachidZaim: cvfit\$lambda.min is 0.05074383 and cvfit\$lambda.1se is 0.05574419, both 8 remaining covariates but not the same ones. (see https://ibb.co/C9ntYZg). It seems to me that the correlation with the outcome is so small that it's very difficult to extract a good piece of information from it. (see https://ibb.co/gWpnpFC) Thank you for your help!! :) – Giulio Benetti Aug 27 '19 at 09:37
  • @user2974951 Whatever the lambda chosen, the resulting model always tends to perform worse than the glm fit with the same number of covariates. In my example, with only two covariates, the results are all true negative or false negative outcomes, providing a sensitivity of 0. Together with shrinking the number of variables, lasso clearly lower the beta predictors. It then the prediction based on the lasso meaningful? To me, it seems better to use the variables selected from the lambda.1se/min and to rebuild a model with these covariates and a simple logistical fit. Isn't it? – Giulio Benetti Aug 27 '19 at 09:47
  • It's hard to tell whether you are using deviance or classification error as your criterion for cross-validation, as one of your plots shows one and the other the other. Stick with deviance, as classification error is not a [proper scoring rule](https://stats.stackexchange.com/a/359936/28500). Getting a good model of probability as a function of your covariates is your first priority. Please re-do your calculations based on deviance as a criterion throughout, report those results in your question, and report what happens when you use the model returned at `lambda.min`. – EdM Aug 30 '19 at 14:12
  • Also, please specify how many cases you have in each class. Please add this information in an edit to your question rather than in a comment, as comments can sometimes get lost. – EdM Aug 30 '19 at 15:03
  • Shouldn't your model predict probabilities rather than 0 or 1? It seems to me that you get only ones because you discretize an odds ratio that is very close to 1. – Sextus Empiricus Sep 02 '19 at 08:25
  • *"resulting in a fully negative prediction."* this part is not clear to me. – Sextus Empiricus Sep 02 '19 at 08:31
  • by using "predict(fit, s=0.142700, newx= fitXData, type="class")", instead of having the probabilities, I obtain the predicted values from the model. All the predicted values are 1 (= FALSE). The table I reported has only one column titled "1" . In practice the model predicts all the cases to be negative, even though 27/60 should be positive.@MartijnWeterings I slightly edited the post to clarify this point – Giulio Benetti Sep 02 '19 at 09:10

0 Answers0