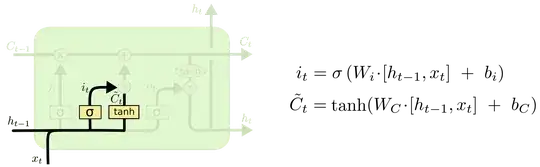
Page 228 of THIS BOOK provides the formula for the variance of the mean of more than two correlated random variables:
where $m$ is the number of variables, $r$ is the correlation between the variables, and $V$ is the variance of each of the variables.
The same book, however, provides a different formula for the variance of the mean of two correlated variables:
The formula formula for more than two variables doesn't seem to be an extension of the formula for two variables. Specifically a $2$ is in the two-variable formula that is absent in the more-than-two-variable formula.
Is this by design?