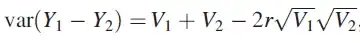Theoretical results. First, an example with results from some theoretical formulas.
Suppose $X_1 \sim \mathsf{Norm}(\mu = 50, \sigma=7),\,$
$X_2 \sim \mathsf{Norm}(40, 5),$ and
$W \sim \mathsf{Norm}(0, 3).$
Then let $Y_1 = X_1 + W,\, Y_2 = X_2 + W$ so that
$$Cov(Y_1,Y_2) = Cov(X_1+W, X_2+W)\\ = Cov(X_1,X_2)+Cov(X_1,W)
+Cov(W,X_2)+Cov(W,W)\\ = 0+0+0+Cov(W,W) = Var(W) = 9$$
because $X_1, X_2,$ and and $W$ are mutually independent. Moreover, by independence, $Var(Y_1) = Var(X_1) + Var(W) = 7^2 + 3^2 = 58$ and, similarly, $V(Y_2) = 34,$ so that
$$Var(Y_1 - Y_2) = Var(Y_1) + Var(Y_2) - 2Cov(Y_1, Y_2) = 58 + 34 - 2(9) = 74.$$
Approximation by simulation. If we simulate a million realizations each
of $X_1, X_2,$ and $W$ in R, then we can approximate some key
quantities from the theoretical results. [R parameterizes the normal distribution in terms of $\mu$ and $\sigma.]$
With a million iterations, it is reasonable to expect approximations accurate to three
significant digits for standard deviations and about two for variances and
covariances. [The weak law of large numbers promises convergence, the central limit theorem allows computations of margin of simulation error based on sample size.]
set.seed(2019); m = 10^6
w = rnorm(m, 0, 3)
x1 = rnorm(m, 50, 7); x2 = rnorm(m, 40, 5)
sd(w); sd(x1); sd(x2)
[1] 3.003595 # aprx SD(W) = 3
[1] 6.994074 # aprx SD(X1) = 7
[1] 4.997491 # aprx SD(X2) = 5
y1 = x1 + w; y2 = x2 + w
cov(y1,y2); cor(y1,y2)
[1] 9.028998 # aprx Cov(Y1,Y2) = 9
[1] 0.2033905
sd(y1); sd(y2); sd(y1 - y2)
[1] 7.61474
[1] 5.829802
[1] 8.597258
var(y1); var(y2); var(y1 - y2)
[1] 57.98426 # aprx V(Y1) = 58
[1] 33.98659 # aprx V(Y2) = 34
[1] 73.91285 # aprx V(Y1 - Y2) = 74
Note: In case you don't know the 'back story' involving random variables $X_1, X_2,$ and $W,$ but you do know the correlation $\rho$
between $Y_1$ and $Y_2,$ here is a way to simulate two normal random variables with a specified correlation $\rho.$ (See this Q&A for discussion.)
If $Z \sim \mathsf{Norm}(0,1)$ and, independently
$Y_2 \sim \mathsf{Norm}(0,1),$ then random variables
$Y_1 = \rho Y_2 + \sqrt{1-\rho^2}Z$ and $Y_2$ have
correlation $\rho.$
set.seed(804); n = 10^6; rho = .8
z = rnorm(n); y2 = rnorm(n)
y1 = rho*y2 + sqrt(1-rho^2)*z
mean(y1); sd(y1)
[1] 0.0005254835 # aprx E(Y1) = 0
[1] 0.9987712 # aprx SD(Y1) = 1
cor(y1,y2)
[1] 0.7998153 # aprx rho = Cor(Y1. Y2) = 0.8