Why is a mixture of two normally distributed variables only bimodal if their means differ by at least two times the common standard deviation?

Question

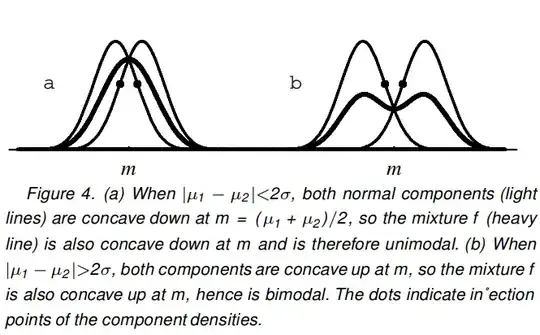
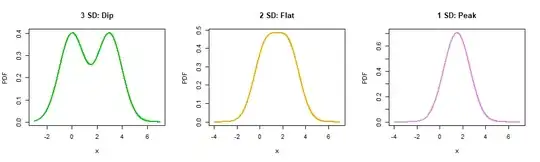
Under mixture of two normal distributions:

https://en.wikipedia.org/wiki/Multimodal_distribution#Mixture_of_two_normal_distributions

"A mixture of two normal distributions has five parameters to estimate: the two means, the two variances and the mixing parameter. A mixture of two normal distributions with equal standard deviations is bimodal only if their means differ by at least twice the common standard deviation."

I am looking for a derivation or intuitive explanation as to why this is true. I believe it may be able to be explained in the form of a two sample t test:

$$\frac{\mu_1-\mu_2}{\sigma_p}$$

where $\sigma_p$ is the pooled standard deviation.

Answer 1

This figure from the the paper linked in that wiki article provides a nice illustration:

The proof they provide is based on the fact that normal distributions are concave within one SD of their mean (the SD being the inflection point of the normal pdf, where it goes from concave to convex). Thus, if you add two normal pdfs together (in equal proportions), then as long as their means differ by less than two SDs, the sum-pdf (i.e. the mixture) will be concave in the region between the two means, and therefore the global maximum must be at the point exactly between the two means.

Reference: Schilling, M. F., Watkins, A. E., & Watkins, W. (2002). Is Human Height Bimodal? The American Statistician, 56(3), 223–229. doi:10.1198/00031300265

Answer 2

This is a case where pictures can be deceiving, because this result is a special characteristic of normal mixtures: an analog does not necessarily hold for other mixtures, even when the components are symmetric unimodal distributions! For instance, an equal mixture of two Student t distributions separated by a little less than twice their common standard deviation will be bimodal. For real insight then, we have to do some math or appeal to special properties of Normal distributions.

---

Choose units of measurement (by recentering and rescaling as needed) to place the means of the component distributions at $\pm\mu,$ $\mu\ge 0,$ and to make their common variance unity. Let $p,$ $0 \lt p \lt 1,$ be the amount of the larger-mean component in the mixture. This enables us to express the mixture density in full generality as

$$\sqrt{2\pi}f(x;\mu,p) = p \exp\left(-\frac{(x-\mu)^2}{2}\right) + (1-p) \exp\left(-\frac{(x+\mu)^2}{2}\right).$$

Because both component densities increase where $x\lt -\mu$ and decrease where $x\gt \mu,$ the only possible modes occur where $-\mu\le x \le \mu.$ Find them by differentiating $f$ with respect to $x$ and setting it to zero. Clearing out any positive coefficients we obtain

$$0 = -e^{2x\mu} p(x-\mu) + (1-p)(x+\mu).$$

Performing similar operations with the second derivative of $f$ and replacing $e^{2x\mu}$ by the value determined by the preceding equation tells us the sign of the second derivative at any critical point is the sign of

$$f^{\prime\prime}(x;\mu,p) \propto \frac{(1+x^2-\mu^2)}{x-\mu}.$$

Since the denominator is negative when $-\mu\lt x \lt \mu,$ the sign of $f^{\prime\prime}$ is that of $-(1-\mu^2 + x^2).$ It is clear that when $\mu\le 1,$ the sign must be negative. In a multimodal distribution, however (because the density is continuous), there must be an antimode between any two modes, where the sign is non-negative. Thus, when $\mu$ is less than $1$ (the SD), the distribution must be unimodal.

Since the separation of the means is $2\mu,$ the conclusion of this analysis is

A mixture of Normal distributions is unimodal whenever the means are separated by no more than twice the common standard deviation.

That's logically equivalent to the statement in the question.

Answer 3

Comment from above pasted here for continuity:

"[F]ormally, for a 50:50 mixture of two normal distributions with the same SD σ, if you write the density $$f(x)=0.5g_1(x)+0.5g_2(x)$$ in full form showing the parameters, you will see that its second derivative changes sign at the midpoint between the two means when the distance between means increases from below 2σ to above."

Comment continued:

In each case the two normal curves that are 'mixed' have $\sigma=1.$ From left to right the distances between means are $3\sigma, 2\sigma,$ and $\sigma,$ respectively. The concavity of the mixture density at the midpoint (1.5) between means changes from negative, to zero, to positive.

R code for the figure:

par(mfrow=c(1,3))
  curve(dnorm(x, 0, 1)+dnorm(x,3,1), -3, 7, col="green3", 
    lwd=2,n=1001, ylab="PDF", main="3 SD: Dip")
  curve(dnorm(x, .5, 1)+dnorm(x,2.5,1), -4, 7, col="orange", 
    lwd=2, n=1001,ylab="PDF", main="2 SD: Flat")
  curve(dnorm(x, 1, 1)+dnorm(x,2,1), -4, 7, col="violet", 
    lwd=2, n=1001, ylab="PDF", main="1 SD: Peak")
par(mfrow=c(1,3))