Distribution with 3 Modes, Find the 2 In-Between Minima

Question

Suppose I have a dataset consisting of numbers drawn from three normal distributions $\mathcal N\!(\mu_{\rm left}, \sigma_{\rm left}^2),\ \mathcal N\!(\mu_{\rm center}, \sigma_{\rm center}^2),\ \mathcal N\!(\mu_{\rm right}, \sigma_{\rm right}^2)$. The task is to decide for each data point whether to classify it as left, center or right within a computer program (specifically Python), without relying on human eye-balling.

The professor suggested drawing a histogram, identifying the $3$ peaks, and drawing cutoff lines at the minima between the peaks.

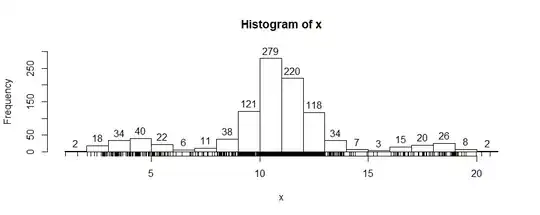
So how to implement this exactly? My idea was to partition the data into $20$ bins of equal width. The left endpoint of the first bin I set as the smallest value in the data set and the right endpoint of the last bin I set as the largest value in the data set. I then make a list of the number of data points in each bin. In the example I generated, that list is:

[2, 18, 34, 40, 22, 6, 11, 38, 121, 279, 220, 118, 34, 7, 3, 15, 20, 26, 8, 2]

If I could rely on human eyeballing, it's easy to see that the peaks occur at 40, 279 and 26 and the inter-peak minima occur at 6 and 3. I could then just draw the cut-off lines at the centers of the bins corresponding to those minima.

But since I can't rely on eyeballing? Then I have to ask the computer to pick out the $3$ peaks. But I can't just pick out the $3$ biggest bins; that would yield 279, 220 and 121 instead of the desired 40, 279 and 26. Another idea would be to make a list of $[\text{next bin size} - \text{current bin size}]$ and look for places where that changes sign. While this would work in my specific example, I could imagine it getting thrown off by a bit of noise. For instance, what if my list of bin sizes had started off with 2, 18, 34, 40, 22, 23, 6, etc?

Any suggestions?

Answer 1

I will mention several approaches that come to mind with illustrations in R. Maybe some of them will match with contents of your course and some can be easily done in Python.

First, here is a histogram of data that I assume (from your comment) is somewhat like yours. The binning in most software depends on the sample size and range of the data, and you cannot generally rely that tallest histogram bars will correspond to centers of the three distributions being mixed.

hist(x, prob=T, br=20, col="skyblue2");  rug(x)
 lines(density(x, adj=2), lwd=2, col="red")

The red curve is a kernel density estimate (KDE) of the overall population. I have used R's default density estimator. In R, the output of 'density' gives x and y-vectors. You might scan the values of the y-vector to find its relative maxima, find the corresponding x-locations, and put 'classification' barriers at troughs between the lower and central and between central and higher 'humps'.

Notice that this method does not apportion your 1024 observations into three groups of about 340 observations. If there is an unstated assumption that the three constituent distributions are sampled with equal probability, you will have to take that information into account in making your classification.

The rug shows locations of points (with overplotting for ties). You can get an idea of their locations by sorting the data. And you might take differences of the sorted data, looking for two relatively large gaps.

Your idea of listing the frequencies in the various bins seems reasonable. Here is a frequency histogram with the frequency of each bin shown atop the appropriate bar. For these data, in which the separation of the three categories is quite distinct, the list of frequencies seems a good guide to to locating peaks and troughs. However, in general I think KDEs would be more reliable.

Here is another histogram of exactly the same data, but R's default choice of bins. The boundaries of the three categories would not be much different.

However, the KDE does not change as histogram binning changes. The exact maximum of the KDE is at 10.589. By taking differences of the y.den values one can also find exact locations of troughs.

x.den = density(x)$x; y.den = density(x)$y
x.den[y.den == max(y.den)]
[1] 10.58938

In certain circumstances KDEs or lists of frequencies may substitute for human eyeballs in classification by component. There are also some clustering and discrimination methods I have not mentioned here. I don't know anything about your course, but this problem may be an invitation to look ahead in the textbook for methods that may be coming soon.

Finally, as an additional potential complication, you should know that not all mixture distributions will show noticeable dips (in the histogram or KDE) nor noticeable gaps (in between tick marks or sorted observations).

For example, if three normal distributions all have the same standard deviation, then you will see dips or gaps only when the means differ by more than two standard deviations. (Reference.) If standard deviations and probabilities of components differ, then the rules for visible gaps are more intricate.

set.seed(4321)
x1 = rnorm(100,50,5); x2 = rnorm(100,75,5); x3 = rnorm(100,85,5)
x = c(x1,x2,x3)
hist(x, prob=T, col="skyblue2");  rug(x)
 lines(density(x), lwd=2, col="red")