NLS model comparisons by ANOVA

Question

I am comparing NLS models from two groups, males and females. I compared the models by ANOVAs, but I am hesitating which is the correct model comparison to use:

a) Subgroup Males vs Subgroup Females

b) All data (males and females) vs Subgroup Males (the smaller group in terms of sample size)

Bates and Pinheiro mentioned in their book, in chapter 8, to use the smaller group vs the whole sample. But, their example involved more than 2 groups.

I received the suggestion to add my code, so here it is:

I am using the von Bertalanffy growth function and the nlstools package from R:

function (t, Linf, K = NULL, L0 = NULL) { if (length(Linf) == 3) { K <- Linf[[2]] L0 <- Linf[[3]] Linf <- Linf[1] } Linf - (Linf - L0) * exp(-K * t) }

Based on the Kumura (2015) paper and equations: LIKELIHOOD METHODS FOR THE VON BERTALANFFY GROWTH CURVE

Subsetting the data "df" into:

Males_df and Females_df

Stating the initial parameters with the vbsStarts Function in R:

svTLength_All <- vbStarts(Length~Age,data=df,type="vonBertalanffy")

svTFemales_Length<- vbStarts(Length~Age,data=Females_df,type="vonBertalanffy")

svTMales_Length<- vbStarts(Length~Age,data=Males_df,type="vonBertalanffy")

Fitting the models with those values:

fitLength_All <- nls(Length~vbT(Age,Linf,K,L0),data=df,start=svTLength_All)

fitLength_Females <- nls(Length~vbT(Age,Linf,K,L0),data=Females_df,start=svTFemales_Length)

fitLength_Males <- nls(Length~vbT(Age,Linf,K,L0),data=Males_df,start=svTMales_Length)

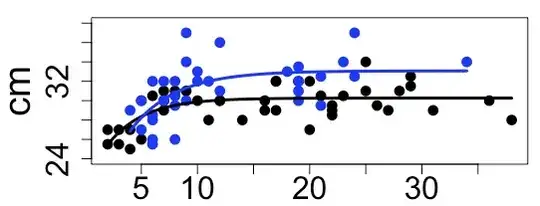
The sample sizes are n=42 for Females and n=35 for males.

The plot looks like this (x axis = Age in months):

I want to know if the difference between the growth curves from males and females is statistically significant.

I understand that an ANOVA between NLS models should include a hierarchical relation and Bates and Pinheiro mention, in chapter 6 from their book, that the best is to compare the model including the full data (fitLength_All, in this case) to the model estimated from the smaller group (fitLength_Males, in this case).

So I compared:

anova(fitLength_All, fitLength_Males)

I am still not sure that this is the best way to compare males vs females. For me taht anova would mean if males are the overall population are te same. When I do teh same for females:

anova(fitLength_All, fitLength_Females)

or between males and females:

anova(fitLength_Males, fitLength_Females)

The results vary greatly. I am not fully comfortable reporting differences only if the anova was significant between "All" (df) and the subgroup males [anova(fitLength_All, fitLength_Males)]. I am looking for advice on how to compare those growth curves statistically or for reassurance in case that anova is the correct way. If so, how may I interpret it?