I would like to figure out which distribution fits my data best.
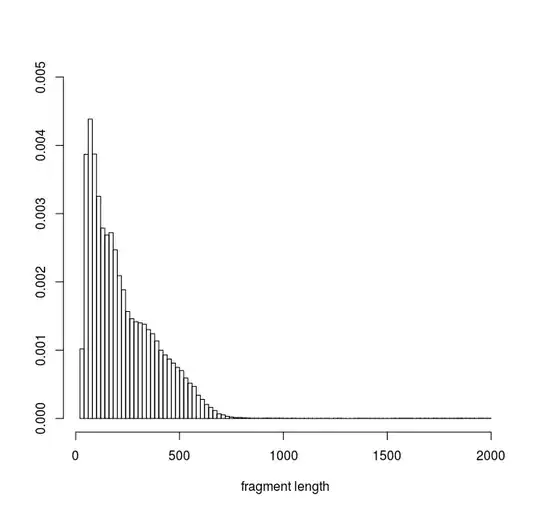
Here is the histogram of my data :
I used the fitdistrplus package in R to try to find the best fit for my data.
To get an idea of which family distribution to fit, I did this:
library(fitdistrplus)
descdist(my_data, discrete=FALSE, boot=500)
I get this skewness-kurtosis plot :
With these summary statistics :
min: 23 max: 1989
median: 184
mean: 228.8346
estimated sd: 165.6273
estimated skewness: 1.706379
estimated kurtosis: 11.31023
So apparently no distribution is a good candidate for the data. How to interpret this plot ? Does this mean that my data is a mixture of several distributions ?
EDIT :
This distribution represents DNA fragment lengths obtained from an experiment. My aim is to be able to simulate the result of this experiment by simuating the resulting fragments. (i.e a simulated fragment is defined by two positions in the genome seperated by a distance D). I assume that the fragment length distribution observed from the real experiment can be described by a density function or a mxiture of densities. I am looking fo the best function from which I could sample values of D for my simulations.
To note, I am using only a sub sample to fit a distribution. We generate millions of fragments. I work on subsample of 500.000 fragments.