5

Finding a distribution of the data is a crucial part of my thesis. I have to process this step in R eventhough there are some other tools to get these information in fast. I made some search to analyze which distribution fits best for the given variable, this instructions guided me a bit.

For instructions: via stackoverflow: how-to-determine-which-distribution-fits-my-data-best

However, I am lost to have distributions of the variables since I have about 18.

For example;

http://www.filedropper.com/samplest

library(fitdistrplus)   

importeddata <- read.csv(file.choose(), sep=";",na.strings = "", stringsAsFactors=FALSE, header = TRUE)

for(i in 1:tail(ncol(importeddata))){
  importeddata[,i] <- gsub(",", ".", importeddata[ , i])} 
xx<- as.matrix(as.data.frame(lapply(importeddata, as.numeric)))

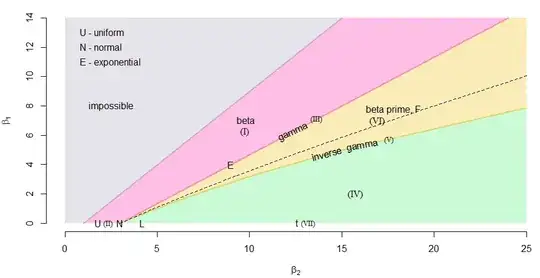
descdist(xx[,1])

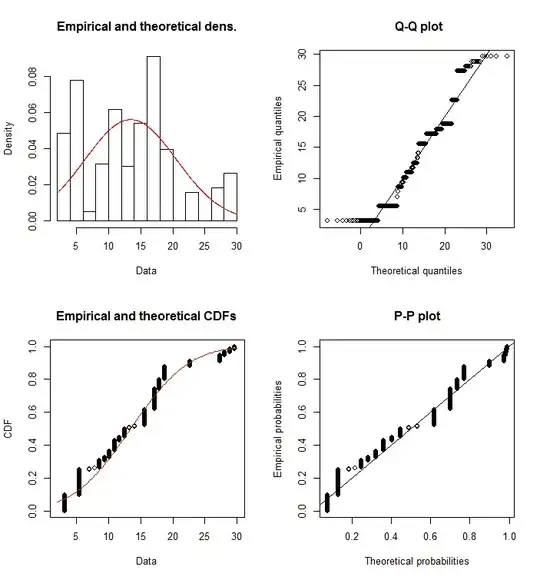
enter image description here

I can say that this variable may fit uniform, beta or normal distributions. Let's see.

    fit.norm <- fitdist(xx[,1], "norm")
    fit.norm
         Fitting of the distribution ' norm ' by maximum likelihood 
         Parameters:
              estimate Std. Error
         mean 13.428316  0.3652664
         sd    7.120353  0.2582823

    plot(fit.norm)

enter image description here

However, beta causes an error. Because, the beta distribution is a family of continuous probability distributions defined on the interval [0, 1] parametrized by two positive shape parameters, denoted by α and β, that appear as exponents of the random variable and control the shape of the distribution.

   fitdist(xx[,1], "beta")

Error in start.arg.default(data10, distr = distname) : values must be in [0-1] to fit a beta distribution

  fit.uni <- fitdist(xx[,1], "beta")

       Fitting of the distribution ' unif ' by maximum likelihood 
       Parameters:
        estimate Std. Error
             min     3.12         NA
             max    29.64         NA

   plot(fit.uni)


  fit.uni$aic
  [1] NA

  fit.norm$aic
  [1] 2574.241

There are two questions to be asked:

  1. May I directly said that xx variable is normally distributed N(13.42,7.12)? How can I compare the distributions better or not?
  2. Is there alternative way to have these informations? Because it is going to be repeated 18 times.
Glen_b
  • 257,508
  • 32
  • 553
  • 939
can.u
  • 51
  • 1
  • 3
  • 1. *Why* is it necessary to identify a distribution? What are you using this to do? 2. Why consider only those particular distributions and not others? – Glen_b Sep 21 '16 at 11:56
  • 3. Your data look to be distinctly discrete. Have they been binned? What do the numbers represent? – Glen_b Sep 21 '16 at 12:48
  • @Glen_b This data had been gathered for market research which includes, duration, and the answers of the participants for asked question. I wanted to analyze normal, uniform and gama, since obersvation is close to them. I do not know exactly how can I find a distribution of raw data. That's why I may be looked as lost. – can.u Sep 21 '16 at 18:54
  • @Glen_b as you said I need to evaulate data for other distributions. Should I follow the code of following link? http://stackoverflow.com/questions/2661402/given-a-set-of-random-numbers-drawn-from-a-continuous-univariate-distribution-f – can.u Sep 21 '16 at 19:05
  • You don't explain how your data come to be discrete (yet somehow not integer); this discreteness may be an issue for all of your above choices. I don't want to recommend anything without understanding in detail how that discreteness arises for each variable. It's also still not clear what you need to fit a distributional form *for*. What are you going to do with it? What do you need a named distribution for that you couldn't get from the ECDF? – Glen_b Sep 21 '16 at 23:23
  • In response to your second comment: I did *not* say you need to evaluate other distributions. I asked why you chose the ones you did rather than something else. I sought insight into your reasons for choosing those vs some other possibility as a way of trying to get *some* idea what you're trying to achieve with all this. You should *not* follow the code at that link. Thinking is required here, not throwing a bunch of formulas at your data and trying to find something that sticks. – Glen_b Sep 21 '16 at 23:27
  • I'd like to understand how series A, for example, has a lot of "12.48" values. (Also, unless I am confused, your P-P plot looks like your axes are swapped.) – Glen_b Sep 21 '16 at 23:53

1 Answers1

3

There are important things to say that are much too long for comments but you'll need to answer some questions (which I will post in comments) for a proper answer to be offered.

Note that the distributions in the $(\beta_1,\beta_2)$ plot$^\dagger$ are all actually location-scale families of distributions (you can shift or stretch the distributions without changing the skewness and kurtosis).

[In reality in that diagram we're dealing there with the Pearson distributions plus lognormal and logistic; if you're going to show additional distributions than the Pearson family it's not clear to me why you'd add those but not some others; adding new distributions to such plots is discussed here]

The grey region in your plot (pink in the plot below) is that for the Pearson distribution type I -

![Pearson distribution plot
(plot taken from my answer at the link above)

$$f_Y(y) =\frac{1}{B(\alpha,\beta)} \frac{(y-a)^{\alpha-1} (c-y)^{\beta-1}}{(c-a)^{\alpha+\beta-1}},\: a < y <c$$

This is why your beta fit failed!

May I directly say that the xx variable is normally distributed N(13.42,7.12)

It surely isn't, so you had better not claim that it is. It very likely won't from be any of the distributions you consider (nor any other simple distribution). Those are models -- convenient but hopefully useful approximations.

$\dagger$ such charts - plotting sample $\beta_1,\beta_2$ (or sometimes skewness and kurtosis rather than squared-skewness and kurtosis) to identify plausible distributions - long predate Cullen and Frey (1999), by the way; I was making such plots in the 80s (several times, including in an unpublished thesis, though my plot also included the Laplace in addition to the lognormal and logistic that the above plot adds to the Pearson family); but Bowman and Shenton were effectively making them in the 70s, when they ivestigated the sampling distribution of skewness and kurtosis under normality -- and I am pretty confident that Bowman and Shenton didn't come up with the idea of looking at the sample values on a plot like that either; I think it may go back decades earlier. Indeed it turns out Cullen and Frey themselves say "many texts provide such charts" and give the example of Hahn and Shapiro, 1967 (so this oddness is not Cullen and Frey's fault). Some other programs call it a Pearson plot, a much better choice I think.

Glen_b
  • 257,508
  • 32
  • 553
  • 939