How do I find peaks in a dataset?

Question

If I have a data set that produces a graph such as the following, how would I algorithmically determine the x-values of the peaks shown (in this case three of them):

Answer 1

A general approach is to smooth the data and then find peaks by comparing a local maximum filter to the smooth. In R:

    argmax <- function(x, y, w=1, ...) {
      require(zoo)
      n <- length(y)
      y.smooth <- loess(y ~ x, ...)$fitted
      y.max <- rollapply(zoo(y.smooth), 2*w+1, max, 
                align="center")
      delta <- y.max - y.smooth[-c(1:w, n+1-1:w)]
      i.max <- which(delta <= 0) + w
      list(x=x[i.max], i=i.max, y.hat=y.smooth)
    }

Its return value includes the arguments of the local maxima (x)--which answers the question--and the indexes into the x- and y-arrays where those local maxima occur (i).

There are two parameters to be tuned to the circumstances: w is the half-width of the window used to compute the local maximum. (Its value should be substantially less than half the length of the array of data.) Small values will pick up tiny local bumps whereas larger values will pass right over those. Another--not explicit in this code--is the span argument of the loess smoother. (It is typically between zero and one; it reflects a window width as a proportion of the range of x values.) Larger values will smooth the data more aggressively, making local bumps disappear altogether.

To see this tuning in effect, let's create a little test function to plot the results:

    test <- function(w, span) {
      peaks <- argmax(x, y, w=w, span=span)
      
      plot(x, y, cex=0.75, col="Gray", main=paste("w = ", w, ", 
              span = ", span, sep=""))
      lines(x, peaks$y.hat,  lwd=2) #$
      y.min <- min(y)
      sapply(peaks$i, function(i) lines(c(x[i],x[i]), c(y.min, 
             peaks$y.hat[i]),
             col="Red", lty=2))
      points(x[peaks$i], peaks$y.hat[peaks$i], col="Red", pch=19, 
              cex=1.25)
    }

Here are a few experiments applied to some synthetic, slightly noisy data.

    x <- 1:1000 / 100 - 5
    y <- exp(abs(x)/20) * sin(2 * x + (x/5)^2) + cos(10*x) / 5 + 
              rnorm(length(x), sd=0.05)
    par(mfrow=c(3,1))
    test(2, 0.05)
    test(30, 0.05)
    test(2, 0.2)

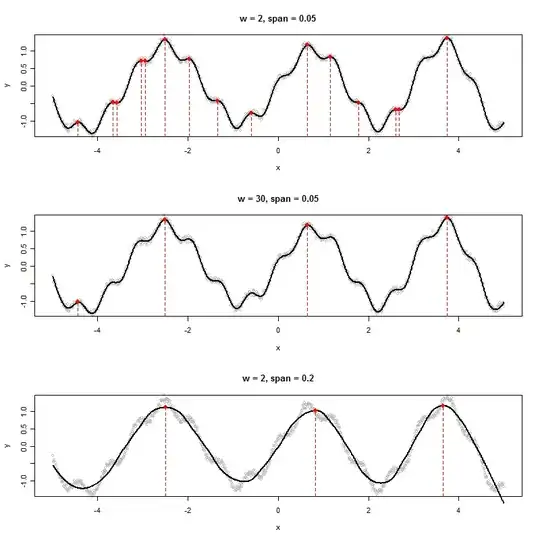
Either a wide window (middle plot) or more aggressive smooth (bottom plot) eliminate the local maxima detected in the top plot. The best combination here is likely a wide window and only gentle smoothing, because aggressive smoothing appears to shift these peaks (see the middle and right points in the bottom plot and compare their locations to the apparent peaks of the raw data). In this example, w=50 and span=0.05 does a great job (not shown).

Notice the local maxima at the endpoints are not detected. These can be inspected separately. (To support this, argmax returns the smoothed y-values.)

---

This approach has several advantages over more formal modeling for general purpose work:

• It does not adopt any preconceived model of the data.

• It can be adapted to the data characteristics.

• It can be adapted to detect the kinds of peaks one is interested in.

Answer 2

A classic peak detection approach in signal processing is as follows:

1. Filter the signal to some reasonable reasonable range, depending on sampling rate and signal properties, e.g. for ECG, an IIR bandpass filter @0.5-20Hz, a zero-phase filter will ensure that no phase shift (and associated time lag) is introduced
2. A hilbert transform or a wavelet approach can then be used to emphasize the peaks
3. A static or dynamic threshold can then be applied, where all samples above the threshold are deemed peaks. In the case of a dynamic threshold, it is usually defined as a threshold N standard deviations above or below a moving average estimate of the mean.

Another approach that works is to compare a sharply highpass filtered signal against a heavily smoothed (low-pass or median filtered) and apply step 3.

Hope this helps.

Answer 3

As I mentioned in comment if the time series appears to be periodic fitting a harmonic regression model provides a way to smooth the function and identify the peak by applying the first and second derivative tests. Huber has pointed out a nonparametric test that has advantages when there are multiple peaks and the function is not necessarily periodic. But there is no free lunch. While there are the advantages to his method that he mentions there can be disadvantages if a parametric model is appropriate. That is always the flip side to using nonparametric techniques. Although it avoids parametric assumptions, the parametric approach is better when the parametric assumptions are appropriate. His procedure also does not take full advantage of the time series structure in the data. My approach does but relies on a specific form for the model that assumes periodicity.

I think that while it is appropriate to point out advantages of a suggested procedure it is also important to point out the potential disadvantages. Both my approach and Huber's find the peaks in an efficient manner. However I think his procedure takes a little more work when a local maximum is lower than the previously determined highest peak.